Cube Question
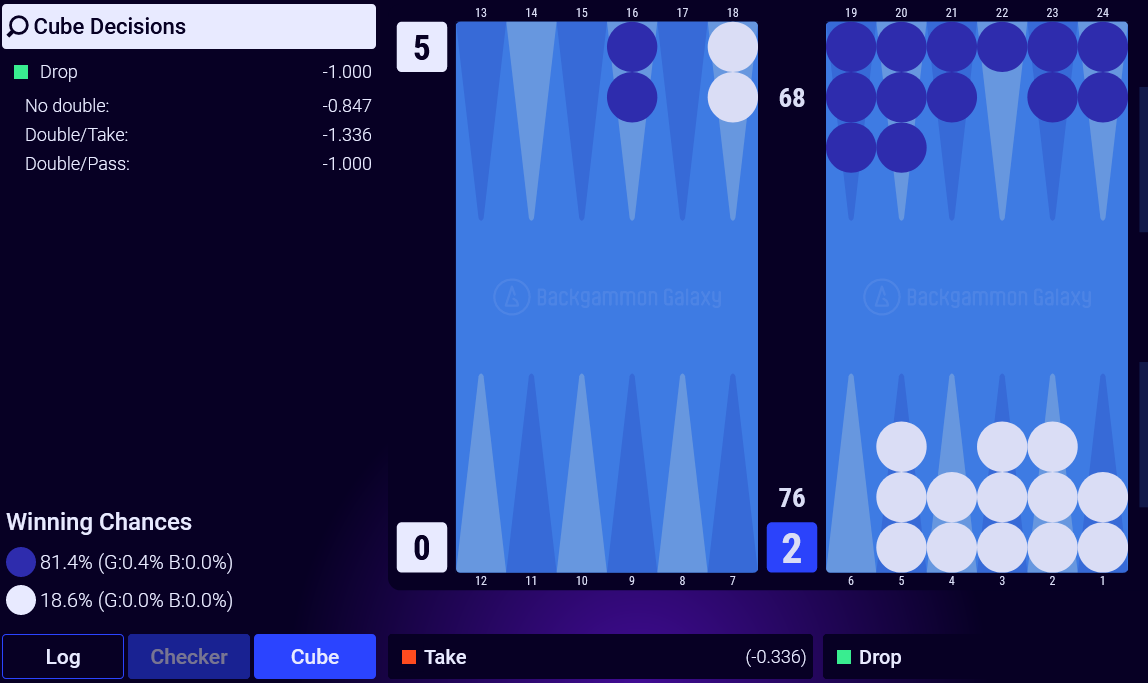
There's something I don't understand about match equity tables. Trailing 0:5 in a 7pt match I took the cube in the position below, which was a big blunder. Dropping the cube I'd get to 0:6 Crawford with 9.3% chance of winning the match per MET, but my chances of winning this game are 18.6%. Can someone explain please?
5 Replies
Your take point is not equal to your MWC after a drop. From the MET I was looking at 6a-1a Crawford is 10% MWC. 3a-2a is 40% (that would be the score you reach is you take, make the mandatory redouble and win the current game).
By passing you can guarantee 10% MWC. Taking risks that 10% for a potential reward of 30% (the 40% MWC you get with a win is 30% higher than the 10% when you pass). Therefore your take point should be risk/(risk+reward), which is 10/40 or 25% in this case. That is why taking with 18.3% game winning chances is a blunder.
Note that the only time your take point is equal to your MWC after a pass would be if you were playing the current game for the whole match. For example if you were trailing 5-3 in a 7 point match, you would win the match if your opponent doubles and you take (remembering to redouble immediately) and go on to win the game. In this case the blunder occurs because winning the current game is not valuable enough to you - it only gives you 40% MWC, not 100%.
thank you very much, i understand now. that was very helpful 😀
follow up question: is the take point calculation (risk/(risk+reward)) the same with a live cube?
The formula must be adjusted for two factors, cube ownership and gammons. Neither were relevant in your OP (losing gammon was meaningless and you were very unlikely to win gammon). As a rule, you can usually drop the take point a few percent for cube ownership. For example, in a money game your risk is 1 (-1 for drop, -2 if you take and lose) while your reward is 3 (-1 for drop vs +2 for taking and winning). Your take point is therefore 1/4 or 25%. The cube is usually live in money play (be careful; there are some positions where the game will be decided on the next roll, and they are not always at the end of the game) so everything I’ve read suggests a take point of 23% or so is more appropriate.
Gammons technically would use a similar formula, just with gammon probabilities factored in to both the risk and reward calculation. In practice, it gets complicated so it’s easier to simply adjust our take point upward when we are at higher risk of losing gammons.
Thank you very much for your help. i see i have a lot to learn ;-)