Fold and Called equity combined
I'm on the turn, I'm contemplating an all-in semibluff and I believe I'm currently behind. How often does the villain need to fold for it to work?
Let's say there are 100bb in the pot and I'm contemplating a 125bb semibluff. Let's say I estimate my pot equity at 25%.
If the villain calls 60% of the time, that means 15% of the time I win 225bb, 45% of the time I lose 125bb and 40% of the time I win 100bb.
15*225 + .4*100 = 37.5 + 40 = 77.5. <==winnings
.45*125 = 56.25 <==losings
So if I have 40% fold equity I show a profit in the long run.
Is my thinking correct so far?
5 Replies
Your opponent must fold more often than the break even percent for your bluff to show an immediate profit . The BEP is bet/(bet+pot). So in the situation you provided the equation would be 125/(125+100) = ~45%.
Your opponent must fold more often than the break even percent for your bluff to show an immediate profit . The BEP is bet/(bet+pot). So in the situation you provided the equation would be 125/(125+100) = ~45%.
That only takes into account the fold equity - he still has 25% equity even when called.
I believe you're thinking about the situation correctly, but your first calculation is off. .15*225=33.75, not 37.5 The total winnings still is higher than the total losses though, so that would be a profitable bet.
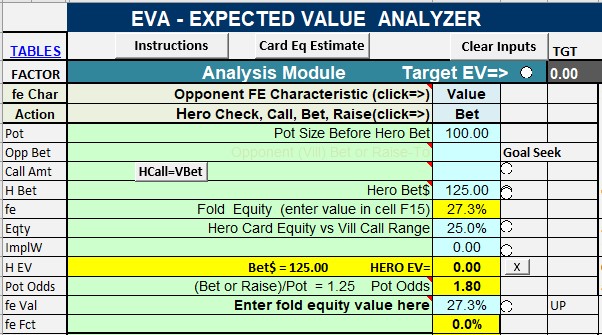
The basic EV equation for a hero bet with fold equity is:
EV = Pr(fold)*Pot +(1-Pr(fold))*(eq*(Pot + 2*Bet)- Bet)
For your example where you bet 125 into a 100 pot with 25% equity and villain folds 40'% of the time, EV = 17.50
If you set EV = 0 , with some algebra (or my gwiz EV program), you will find the break-even fold equity to be 27.3%.
Note: If the bet is not a closing bet such as all-in or the hand is not assumed to be checked down, this will be a first-cut look at EV potential.
Excel is so complicated...