Intuitively understanding mixed value bets

There are two things that can be happening here. First off, it's worth noting that our mixed valuebets almost always (outside of a few niche spots) are on the thinner side. Our strongest linear vbets are basically always pure bets. This means that if we vbet more and bluff more (to prevent the overfold), our strategy can become more vulnerable to jams, as we can never really add hands to our betting range that can comfortably bet/call vs jam - these hands were being vbet anyway.

The second thing has to do with blocker effects. One thing that's a bit less intuitive is that solver is not only balancing a ratio of vbets to bluffs, but is also performing a sort of balancing act against villain's blocker calls. Let's say there's a spot where we're meant to be mixing with JT, pair of tens as our thinnest vbet. If we pure vbet JT, our opponent can start reshuffling their calling range around to gain fractions of ev - bluffcatching with J or T will become relatively better than in gto (assuming bettor adds bluffs to stay balanced), as J is now blocking more of the value range.

Solver tends to get around this by using card matching - that is, solver will add some bluffs with J so the defender's Jx also blocks bluffs (and so doesn't become a favored side card for heroing) - but this isn't always plausible for concrete reasons. So, basically, sometimes messing with our range composition will allow villain to make slightly favorable bluffcatches with some combos, and slightly favorable overfolds with other combos, and thus overperform. One constraint of GTO play is not allowing opponent to make these sorts of deviations, as GTO strat cannot allow villain to make profitable deviations with any combos.

Diving super deep into this stuff is probably not too worthwhile or useful for real play, but more deeply considering blocker interactions is a good skill to develop especially in narrow range spots and to understand equilibrium strat generally.

Thanks very much for the in depth response. On your point that diving super deep into this stuff is not that important - absolutely! I'm not really optimizing for profit here, just interested in learning more about this.

On your first point: this makes sense as far as being the reason that we are indifferent to thin value bets/checks (I'm just going to call mixed vbets thin value). The risk of being punished (either by a call or by a jam/raise) is what reduces our thin value bet EV and makes it equivalent to that of checking. But raising/jamming should be positive EV and therefore done at a pure frequency by our opponent; they have no ability to punish us "even more" if we increase our thin value bet frequency. That's why I guessed that the natural opponent exploit is to call with bluffcatchers less, which I'm willing to believe is negative EV for us (when combined with the jams you mentioned). But I'm not sure if this is correct at all.

On your second point: this is a great explanation, thank you. If we modify the relative proportion of how we allocate our thin value bets, I see how it is exploitable. What what if we increase/decrease the proportion of our thin value bets across the board? Obviously this is a vast simplification - you can't really do this - but if we consider our entire non-pure value range of hands as equal in EV to checking, why are we betting any of them? Is it in service of disrupting the blockers for the actual pure value?

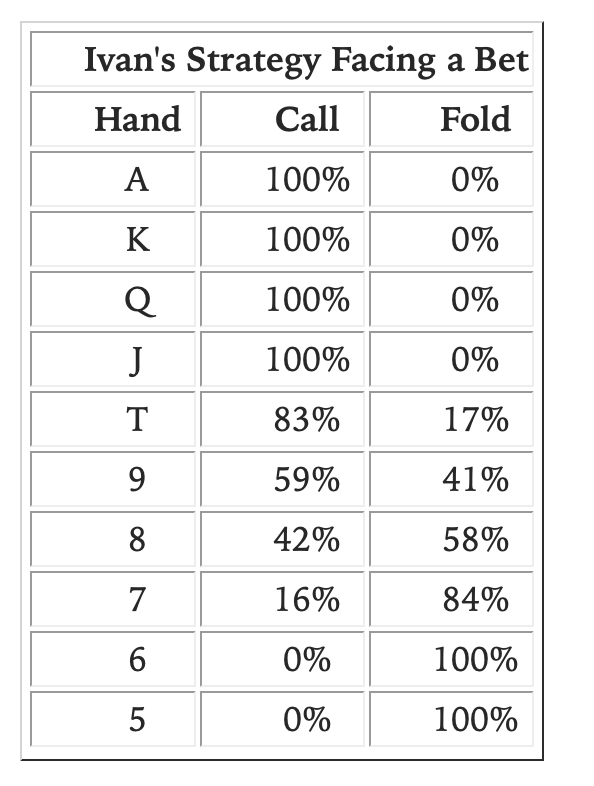
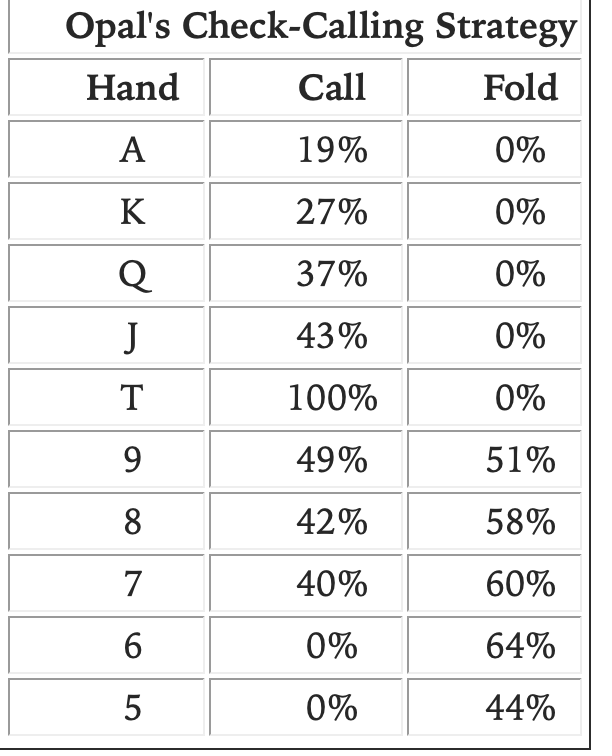
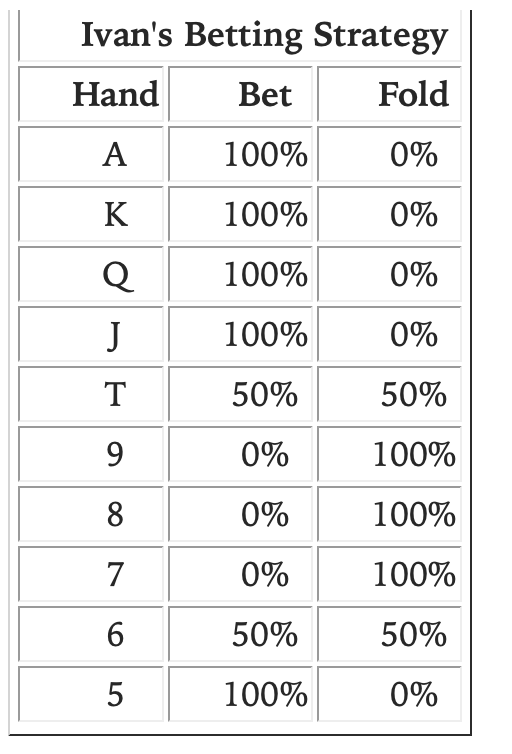
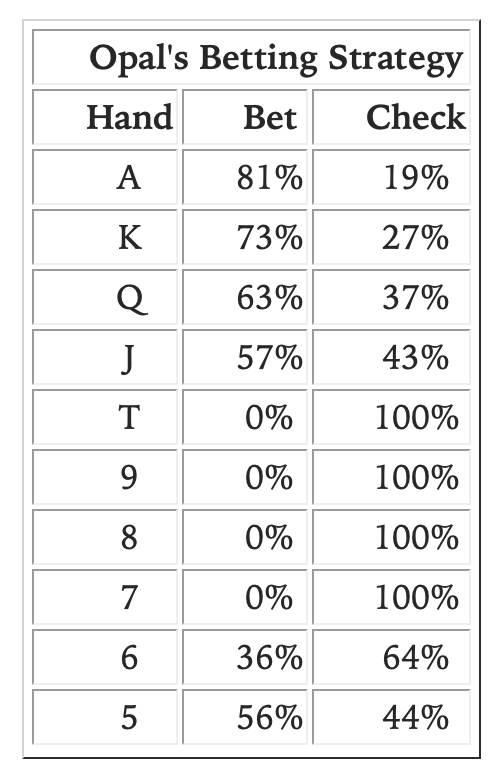
I think even in the absence of blockers, my question holds. Consider the A-5 toy game in Ch. 6 of Play Optimal Poker by Andrew Brokos. I've attached screenshots of the description and equilibrium ranges. I set the situation up in excel; I don't know if I did it exactly right because the EV of bluffing/checking 6s for Ivan is not equal. Overlooking that flaw though, I find that if I set Ivan's betting frequency of T to 0% and 6 to 33% I can achieve indifference across Opal's bluffcatchers 7/8/9/T. Ivan's EV is unchanged. Am I missing now some exploit from Opal?

Similarly, if Ivan bets Ts 100% of the time and 6s 67% of the time he achieves both similar EV and indifference.

Not sure how to share files on this forum. Gdrive?

You can make Opal's 9-7 indifferent if Ivan is betting no T and less 6, or if Ivan is betting more T and more 6. However, what about the ev of Opal's T? Clearly, if Ivan is not adding vbets against T, and he's also bluffing more often, the ev of Opal's T will go up. In order to keep T as an indifferent catcher for Opal, Ivan would have to somehow come up with additional J+ hands to vbet with in order to match the expanded bluffing region. But this is not possible, as Ivan is already pure vbetting all J+ hands. So while Opal's 9-7 bluffcatching range can stay at 0ev, that doesn't mean Opal's entire range gains no ev.

As long as we have a perfectly balanced ratio of vbets to bluffs, we can theoretically set any given range (except for the stone nuts) to be a 0ev catcher. For example, if we only bet the stone nuts and a proportion of bluffs to match our betsize, even the second nuts can be made indifferent - they are losing to the nuts and beating bluffs. But setting a given region of our opponent's range to indifference does not mean the overall range vs range ev will be indifferent unless we are considering a perfectly polarized scenario where the defender's entire range is made up of only bluffcatchers.

If you want to look at the raising stuff more, I'm pretty sure I recall a section on the A-5 game with raises allowed in Brokos' book as well, but I will admit I'm not super sharp when it comes to toy games. However, you should be able to see directly how allowing Opal to raise heavily disincentivizes Ivan from vbetting thinly compared to the call only game. Adding additional thin vbets and bluffs into the range will work in the same direction.

Thank you again for the comments!

Opal's T is not indifferent in the base equilibrium (because it blocks Ivan's thin value T). If Ivan checks all his Ts (and adjusts 6s accordingly) then Opal's T should be indifferent, no? Because T, along with 9-7, beats 5/6 and loses to A-J. I guess I don't understand why either situation is preferable to Ivan.

Also, Ivan's T bet% probably shouldn't matter to Opal's T indifference, because Opal's T blocks Ivan's T. Now, Ivan's T bet% is correlated with his 6 bet%, which matters to Opal's T - which is why in one case Opal's T is indifferent and in another it is a pure call. But it's not clear to me what makes the latter case an equilibrium.

The equilibrium is simply formed when either player cannot unilaterally profit by deviating. There's no a priori way to know what that point will be, it's some mathematical fact that has to be calculated in each spot and in practice depends heavily on the range composition of each player.

Put another way, it's pretty obvious that if Ivan's strategy was just to bet A, and check the rest, Opal's whole range (except A and 5) would be indifferent vs the bet, but also that Ivan is leaving a lot of money on the table by employing this strategy. In this case Opal could also gain a lot of ev by leading more hands as well (Opal leading K will make more money than checking K and being indifferent + almost never facing a bet). So it's clear that this strategy isn't an equilibrium.

Where exactly the lines are for the thinnest vbets isn't something as immediately apparent. But keep in mind there are mathematical realities - getting certain pot odds, Opal will have to call x% of range to prevent Ivan from bluffing ATC. So against Opal's forced defending range, what hands can Ivan profitably vbet? It's a good place to start when understanding toy games.

While mathing this stuff out by hand range vs range is hard, you can math out individual EVs pretty straightforwardly. It might be a good exercise for you to calculate the EV of betting each of Ivan's hands and you can mess around with Opal's defending strategy to see how things change.