Solver selecting actions with identical or even lesser EV
Can anyone explain this?
So say there is an action that has just say 1.01 +ev and so do three other actions. Why does the solver deem one more, or even totally correct over another? Sometimes, it will favor the lesser??? It'll be +1.00 vs +1.01 and it will say the lesser is better. Or they'll all be 1.01 straight down, but it picks one over the other. Is this an error, can someone explain this or put this in to laymen perspective?
There are times it will deem an action OK, other times, the EV difference will be even closer to the "correct" one and it say NO INCORRECT BLUNDER!! again, is this an error? If the difference between +1.01 and +1.45 is "OK" , then how on another action is it +1.44 vs +1.45 a blunder?
To me, +ev is +ev, right?
If I'm checking solver action and as long as my actions are all in +EV, then its at worst, OK to do. Maybe not the best, but I'm still ahead. A lot of times it wants you to be passive. I'm sorry, but passive isn't always the best way to win pots. It also makes you predictable.
Again, any interpretation anyone can give is appreciated.
Also, side note. can anyone explain why you're suppose to 3 bet in the BB with small suited kings, like K4 suited vs UTG? This seems ridiculous.
16 Replies
Error
Can anyone explain this?
So say there is an action that has just say 1.01 +ev and so do three other actions. Why does the solver deem one more, or even totally correct over another? Sometimes, it will favor the lesser??? It'll be +1.00 vs +1.01 and it will say the lesser is better. Or they'll all be 1.01 straight down, but it picks one over the other. Is this an error, can someone explain this or put this in to laymen perspective?
There are times it will deem an action OK, other times, the EV
This is because the solve wasn't done to a high enough accuracy. The ev of any decision in a mixed strategy is the same as any other.
I think these errors won't happen as long as you let the solver run until the highest possible accuracy (down to 0.00), but this might be impractical.
How passive/aggressive you can be, sizings and strategy as a whole depend on range vs range interaction, if you're IP or OOP, etc. Sometimes you have to be very aggressive, others passive. The solver is playing vs itself, it knows each player whole strategy (full clairvoyance), and the result it gives you is the strategy that delivers the max EV. Any deviation you make, because you don't want to play passive because passive is predictable or whatever, won't give you any extra EV vs the solver, and might actually make you lose EV, even if it doesn't adjust anything.
K4s BB vs UTG is part of a polar strategy (strong hands/weak hands). The solver determined a polarized strategy when you're in the BB is the most appropriate for the spot. It's not being 3bet at full frequency, it's a mix as with most hands that are not in the strongest portion of the range. K4s mixes everything, including folds at a small frequency (assuming UTG opens 2.5x, vs a min raise it never folds K4s)
Thank you everyone.
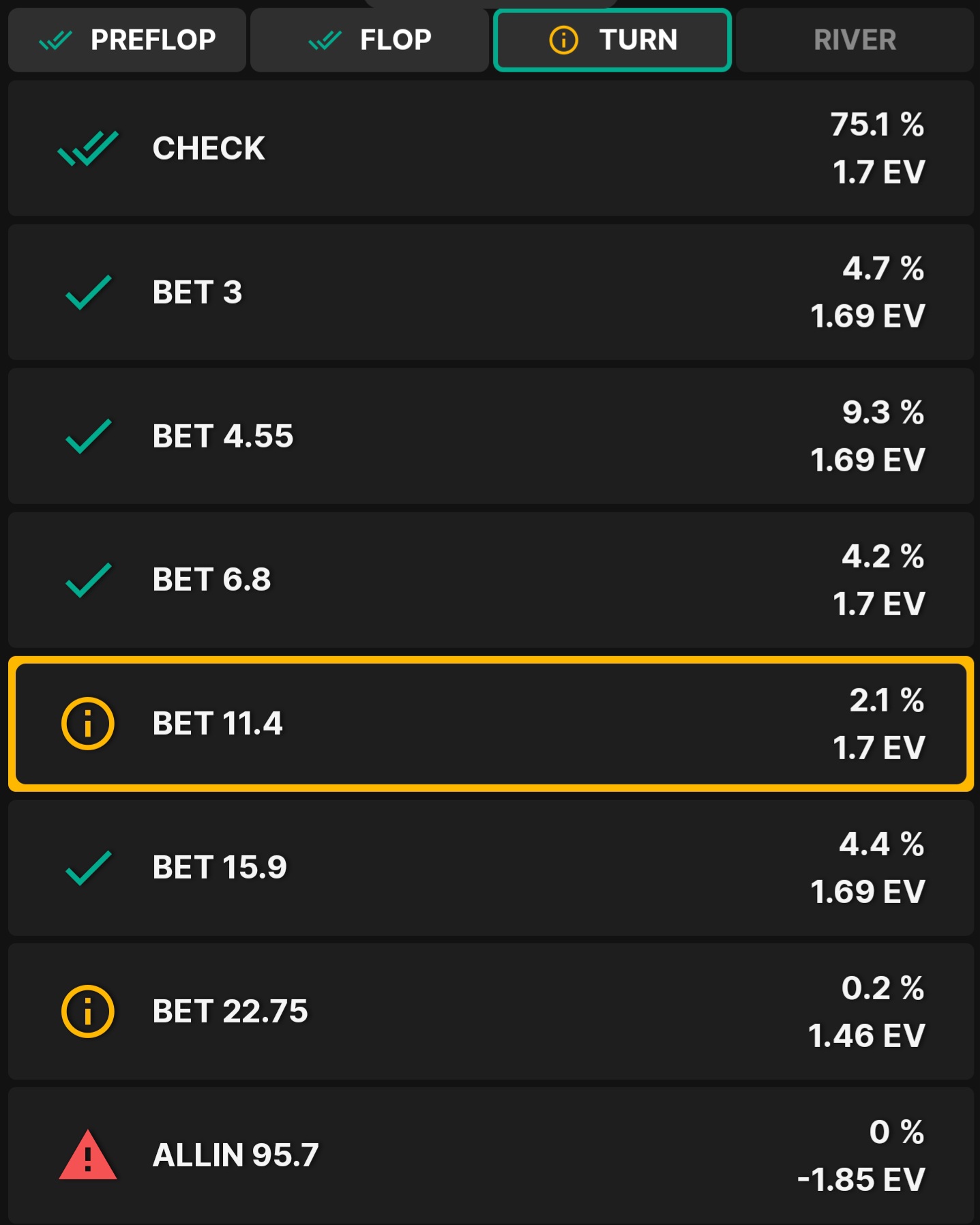
Just to be a full thousand percent clear, [Uploading Image...] I'm going to upload two screenshots as an example. These are from today's training session.
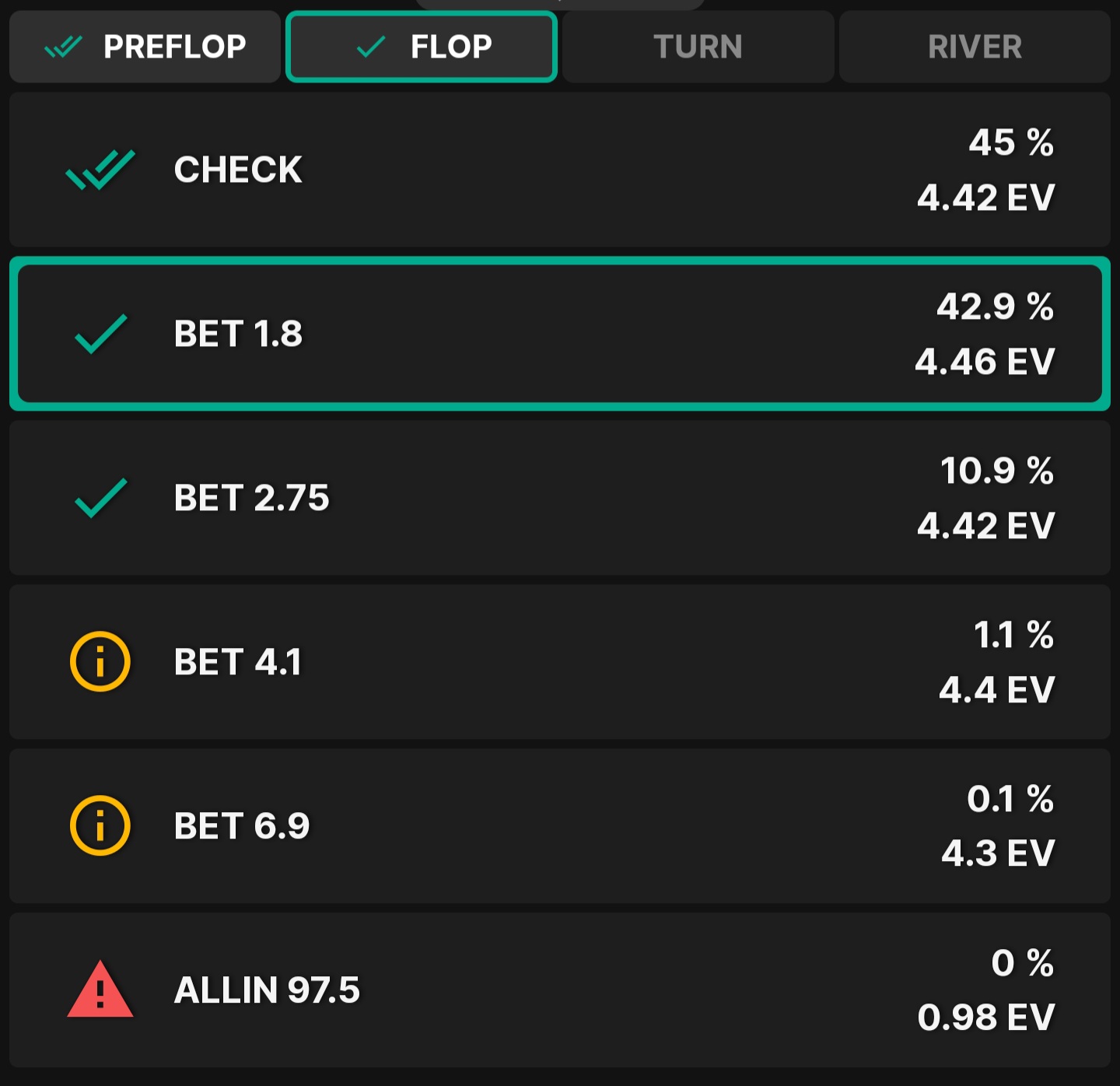
Top image, bet 6.9 is likely an error because it's 0.1% and has a lower ev. Bet 4.1 might be too, difficult to tell. Actions that have really low frequencies like this usually disappear when it's solved for higher accuracy.
Bottom image, bet 11.4 is higher ev than the two other most frequent ones, so it is not an error.
In GTO+ (and I'm assuming other solvers) you can put a filter on the evaluator to tell you that the highest frequency actions are the 'most correct' ones or to filter out anything <5%, etc. I would search around for something like that, but solve to a higher accuracy first. 0.1% DEV usually gets rid of the tiny frequencies.
EDIT: The bottom one looks like a very poorly solved solution, it has something with 20% less ev being bet 0.2% of the time.
The answer: https://blog.gtowizard.com/understanding...
There are a bunch of GTO trainers on the market now, and I've ran into some that have obvious errors. Like for example in one spot a preflop trainer I was using said I should fold Aces, kings and queens and call with jacks. There's also the issue someone mentioned if the solve isn't completed to a high enough accuracy.
That being said, sometimes one option is clearly preferable even though both actions have equal EV.
This is usually a frequency issue. You have to look at the percentage of the time each action is used by the solver. For example one specific hand might not be a mistake to fold (same EV), but if you folded all hands in that class you would be massively overfolding and your opponent could profitably bluff with any two cards.
There are a bunch of GTO trainers on the market now, and I've ran into some that have obvious errors. Like for example in one spot a preflop trainer I was using said I should fold Aces, kings and queens and call with jacks. There's also the issue someone mentioned if the solve isn't completed to a high enough accuracy.
That being said, sometimes one option is clearly preferable even though both actions have equal EV.
This is usually a frequency issue. You have to look at the percentage of the time
Yeah the whole thing is confusing. Every time I get an answer another question pops in to my head lol. I just take the training as a baseline and as a "game" to play. When at the table for real i adjust.
There are a bunch of GTO trainers on the market now, and I've ran into some that have obvious errors. Like for example in one spot a preflop trainer I was using said I should fold Aces, kings and queens and call with jacks.
I dunno about preflop but I mean that's totally a possibility. Calling with unintuitive hands when you fold 'better' hands is something you see in a lot of solves. There are lots of spots where you'd fold AA but call with worse pairs because they're better bluffcatchers vs. your opponents range.
That being said, sometimes one option is clearly preferable even though both actions have equal EV.
In what way? Like practically? If both actions have the same ev then in the equilibrium you're indifferent between the two and can do either.
This is usually a frequency issue. You have to look at the percentage of the time each action is used by the solver. For example one specific hand might not be a mistake to fold (same EV), but if you folded all hands in that class you would be massively overfolding and your opponent could profitably bluff with any two cards.
Sure you'd open yourself up to get exploited by an opponent who can deviate but doing mixed actions pure is not going to lose ev in an equilibrium. I think this is what you're saying but just wanted to clarify.
I dunno about preflop but I mean that's totally a possibility. Calling with unintuitive hands when you fold 'better' hands is something you see in a lot of solves. There are lots of spots where you'd fold AA but call with worse pairs because they're better bluffcatchers vs. your opponents range.
In what way? Like practically? If both actions have the same ev then in the equilibrium you're indifferent between the two and can do either.
Sure you'd open yourself up to get exploited by an opponent who
The spot where the solver wanted me to fold aces, kings and queens but call with jacks was preflop with ICM implications and three people all in ahead of us. It may be some artifact of extremely narrow ranges from opponents, but if it wasn't a mistake from the solver I couldn't figure out why it would do that. Practically speaking it would make no sense for us to play that way.
Regarding your question about frequencies, it does matter. The practical reason for studying GTO is we can play it when we have no idea what our opponent is doing and still at least break even.
That's because for example when we have a bluff catcher we are calling with the optimal frequency so that our opponent is indifferent to bluffing.
But if we fold every bluff catcher and our opponent happens to be over bluffing we are losing EV. Even if they are not intentionally exploiting us our strategy is losing EV, and we are effectively exploiting ourselves.
So if I make a big fold against a good player on the river, I won't look up my exact hand in a solver to justify my play. I will instead look up the range of hands we should be calling with, and ask myself whether I am calling enough in that spot across my whole range. Does that make sense?
A note about using GTO practically speaking: Against good players I often try to replicate GTO to the best of my ability on the flop (and to a lesser extent on the turn).
However by the river I diverge from GTO big time. For the most part there are certain hands that are clear calls or clear folds that sort of play themselves.
However if we've got a bluffcatcher with equal EV for calling or folding, I ask myself whether I think my opponent is over or under bluffing. If they're over bluffing I will call with every bluffcatcher. If they are under bluffing I will fold with every bluffcatcher. That's what the solver would tell us to do if we were to range lock a strategy from our opponent that was over or under bluffing.
Not saying I'm the best at doing this in game, but the best players are good at what I'm describing.
Regarding your question about frequencies, it does matter. The practical reason for studying GTO is we can play it when we have no idea what our opponent is doing and still at least break even.
That's because for example when we have a bluff catcher we are calling with the optimal frequency so that our opponent is indifferent to bluffing.
But if we fold every bluff catcher and our opponent happens to be over bluffing we are losing EV. Even if they are not intentionally exploiting us our strategy i
Well you're kind of saying two different things at the same time here. In an equilibrium, a bluffcatcher is indifferent to folding (when solver mixes), and both folding and calling have an ev of 0, so folding every bluffcatcher (that solver mixes) in an equilibrium actually loses you nothing. Your ev is still 0 whether you call or fold. As I said before, taking a pure strategy from a mixed one does nothing to your ev, unless your opponent takes advantage of it. Also, the polarized opponent constructs his range IP to make you indifferent to calling or folding with your bluffcatchers. You have to call a certain % of the time to prevent him from overbluffing you, but overbluffing in this context means bluffing with hands over and above the ones he would construct a polarized range with. I wouldn't say it makes him 'indifferent' to bluffing you. I would say it prevents him from bluffing with any two cards, just like you said before.
On the other hand, the second situation you describe, where IP is overbluffing, is not an equilibrium. And I think we're saying kind of the same thing: if you fold all your bluffcatchers, you open yourself up to be exploited.
So if I make a big fold against a good player on the river, I won't look up my exact hand in a solver to justify my play. I will instead look up the range of hands we should be calling with, and ask myself whether I am calling enough in that spot across my whole range. Does that make sense?
Sort of, but there's a couple issues with it in my mind. The first issue is that perfectly polarized ranges aren't a thing anywhere but theory (or on rare board textures). The second is that the hands people choose to bluff with (when they do bluff) are quite different from the hands people should be constructing their polarized ranges with. The third is that even if you do find a spot where your opponent is polarized and overbluffing (more frequent) with well constructed ranges, calling more often doesn't gain you ev (at least, not on the combos where solver mixes). Your bluffcatching range is already indifferent to his polarized range. The only reason you call at all is to prevent him from widening that range (bluffing with any two-like you said). If that's what you mean by 'overbluffing' then sure, I guess I agree. If by overbluffing you mean 'more frequent with the same mixed range,' then I do not agree. However, this last sentence I am not as confident on and am open to being proven wrong.
A note about using GTO practically speaking: Against good players I often try to replicate GTO to the best of my ability on the flop (and to a lesser extent on the turn).
What's a good player?
However by the river I diverge from GTO big time. For the most part there are certain hands that are clear calls or clear folds that sort of play themselves.
However if we've got a bluffcatcher with equal EV for calling or folding, I ask myself whether I think my opponent is over or under bluffing. If they're over bluffing I will call with every bluffcatcher. If they are under bluffing I will fold with every bluffcatcher. That's what the solver would tell us to do if we were to range lock a strategy from our opponent that was over or under bluffing.
Not saying I'm the best at doing this in game, but the best players are good at what I'm describing.
I think playing GTO or anything close to it is basically impossible, and even if you could, why would you? 1. no one can be expected to memorize flop frequencies with hundreds of combos across 1755 strategically unique flops and 2. your opponent certainly hasn't memorized his call/fold/CR frequencies across his hundreds of combos across 1755 unique flops either. You should just intuit whatever betsize your opponent makes the biggest mistake with (or use MDA to figure it out) and then do that. For example, why use a polarized bet if your opponent is likely making the biggest overfold compared to MDF facing a b10? You're making a massive relative mistake by choosing to polarize, like solver says, if a b10 gets your opponent to overfold more often, and vice versa.
In response, I'll try to clarify what I meant. Apologies because I'm not always the best at using precise language to get my point across.
I think some people have the misconception that if an action is mixed at equilibrium (according to solver), that you can't lose EV by taking either action. I was trying to explain that this isn't true.
Against a solver your EV won't change. That's because the solver is playing at equilibrium, making it indifferent to your response.
However pretend you're playing against a human that bluffs with every combo on the river, when they should be giving up with a certain percentage.
Now suddenly all of those calls that are break-even against a solver are actually -EV against this player and turn into pure folds. If you node locked your opponent's strategy this would be reflected in the results. This is true even if your opponent is only over bluffing with combos that are mixed-frequency bluffs.
The reason the solver's strategy still can't lose is because it is calling with bluffcatchers at the perfect frequency so that it does not give up EV whether its opponent always bluffs or never bluffs.
Think of it this way, if you're playing rock-paper-scissors against a solver, you could throw any symbol at any frequency and you are going to break even because the solver is randomizing. All symbols are 0 EV.
However if you're playing against a human who throws rock 100% of the time, and you throw scissors more than 1/3 of the time then you are going to lose. Just because scissors is mixed at equilibrium (0 ev either way against a solver) doesn't mean that the frequencies don't matter. If you randomize all symbols appropriately you will still break even, but if you over throw scissors you will lose.
Now a lot of the other stuff you said I actually agree with. You should be playing exploitatively a lot and you're never going to perfectly replicate a solve.
However at the highest stakes the best players actually are pretty good at replicating a solver... And they will definitely notice if you are over or under bluffing/calling/whatever and will take advantage by exploiting you accordingly.
But even if the people you're playing against aren't world class, you can still lose EV just because their natural reaction is to blast away bluffing with everything and your natural reaction is to fold anything that's close (like all the mixed frequency bluffcatchers).
In response, I'll try to clarify what I meant. Apologies because I'm not always the best at using precise language to get my point across.
I think some people have the misconception that if an action is mixed at equilibrium (according to solver), that you can't lose EV by taking either action. I was trying to explain that this isn't true.
Against a solver your EV won't change. That's because the solver is playing at equilibrium, making it indifferent to your response.
However pretend you're playin
We agree and are saying the same thing. I was thrown off because you're describing two different scenarios (one is an equilibrium, and one isn't) but the shift between the two is so quick that I thought you were saying something different.
The question I now have for anyone that knows, because this discussion made me question it: in an equilibrium, is the ratio of bluffs to nuts in a polarized range the thing that makes our opponent indifferent?
Let me elaborate. We know that a person (in an equilibrium) can pure his frequency actions and not lose ev against his opponent (assuming opponent doesn't adjust). Is that statement still true for the polarized opponent? Part of me thinks it must be because the game is in equilibrium, so neither side can deviate to increase their payoff. But then part of me is like well if IP pures his mixed check/bets then he just bluffs more than optimal. Or will IP never have mixes?
I mean I think logically the answer has to be that if the condensed opponent can just fold all his mixed combos because they're equal ev to his calls (0), then the polarized opponent must also be able to pure bet all his mixed bet/checks because they're equivalent ev too. Just trying to wrap my head around how that wouldn't increase his bluffing ratio, or why that wouldn't matter.
Yeah against an opponent who calls at equilibrium frequencies the polarized player (better) can bluff with all of their mixed combos or none of them and their EV gain or loss would still be 0.
That might have been a better example for me to use. It "doesn't matter" what we do because our opponent the solver is perfectly balanced with their calling range to make us indifferent. The solver only gains EV passively if we make blunders by betting hands that should be pure checks or vice versa.
My whole point was that the frequencies in these spots don't matter against a solver but they do matter against a human who isn't perfectly balanced.
So just because a spot is mixed at equilibrium doesn't mean it doesn't matter what we do or at what frequency.
Anyway off to play a tournament, day 1 of a series. Wish me luck 🍀