The problem of GTO max late regging, and a solution
So this starts with an article/Video by GtoWizard in collaboration with an analyst Melcher Malmuth.
The essay explores the question of at what point in a tournament does ICM become so important that it significantly changes the strategy. It's not very mathematically rigorous, and the approach is based on monte carlo simulations. But it there's some significant findings.
https://www.youtube.com/watch?v=sPYbp8Pu...
The experiment consists of two main strategies, one that considers only chipEV and the other tightening aggression frequencies and incorporate chipEV + seatEV differentials.
No surprise that the ICM strategy outperforms, but the experiment tests out mixed strategies where the strategy changes at different points in the tournament.
It turns out that using ICM ranges as early as the first hand greatly outperforms any other strategy.
It makes sense since doubling up in the first hand will have rippling effects throughout the lifetime of the tournament.
So the consequence of this is that, excluding rake and edge considerations, the optimal strategy is to register as late as possible, even if the late registration period doesn't go into the "late" stages of the tournament, I think this isn't very new. But I have been pondering on this since I was qualified to a satellite tournament outside my brm.
The main arguments to register early are usually related to the edge of a player and the rake. Of course that registering late reduces the ROI and increases variance. On the other hand we can safely say that signing late is GTO, and registering early is exploitative. And we would need to see some evidence before judging whether the ROI of early registering is truly higher than late regging, after all the ROI of late regging should be higher against optimal opponents, the effect from edge over weaker opponents would need to be quite strong.
This is without even going into the time savings (if you consider time spent on the tables as a negative) of late regging.
Finally, an implication for Casinos and Tournament Organizers is that there needs to be some incentive for players to register early. Some casinos waive the rake, but I think this is not very clean accountability wise, the Casino still provides services to the player and should be paid for it. I think the best way to fix this would be to pay a bonus in chips to players that arrive on time.
It is even possible, especially as a stage 2 implementation, to change the bonus based on the level. So as to smooth the reward function.
I think this is important not only for the health of the game, but for the health of the players, games are designed (or selected) for features that make players better people, poker entices players to think about maths, statistics, psychology, encourages discipline. Hold'em improves on top of 5 card draw by encouraging more interaction between the players instead of playing solitary.
I propose this early sign up bonus will reward players for being on time, and encourage them to be consistent and punctual in the tables and outside of the tables.
9 Replies
Here is an example of applied theory:
Tournament is 55$ entry or a ticket that we hold. Ticket cannot be exchanged, a corollary of this is that rake is irrelevant to our decision making in this scenario.
The prize pool is 1500$.
First 5 entrants get a 2500$ bundle of tickets.
5-30 get a 100$ ticket.
Assume 300 entrants.
Level structure is blinds go up every 5 minutes (there's antes).
Starts out at 100BB.
Late reg ends after 1 hour, at which point the starting stack is 10BB.
The only possible place a reason to early reg could be hiding (outside of rake and edge), is in the power of strong stacks to bully shorter stacks. I've seen some analysts refer to this as risk premiums.
On utility advantage: this might be an orthogonal phenomenon, but if we have a utility function advantage, say we have a deeper BRM than the average player, or are backed by a stable, or have a stronger risk appetite that the average player. We might be able to gain the EV the other players sacrifice for a more consistent return.
Two more concepts, the game is repeated and we can skip it and rejoin a later one, in this case the ticket does not expire and is repeated in the future, but this applies to any tournament really, since cash is fungible and you can reuse that to register to later tournaments. So we have the choice of not registering to the tournament, we might for example register 50% of the time and apply a free selective pressure to only register for the best 50% tournaments, and we might even tighten up that tournament bumhunting frequency. The variable we would select for would be average stack for starers, the higher the average stack, the better the tournament, but we would probably look for the variance in stacks, two tournaments with 20% of the field busted can be different if everyone has average stacks on one, but on the other there's a lot of chip leaders and a lot of shortstacks.
Finally, we might use this time to watch the tournament, we can see both the individual players as well as the field. If we see a particularly bad player, and the amount of tables isn't very high, we might roll to be seated with that player. Or to be reseated with them.
The end.
Ohhh, Knockouts and bounties fix late reg advantage as well.
An argument for early regging (although it derives from rake and edge arguments)
The GTO solution for cash games is to sit out. If you want to late reg, you can take it a step further and not register (similar to the solution of registering only a fraction of the time).
Both in tournaments and cash, the strategy of table/tournament selection is overpowered, unless you account for time cost. It is similar to a blindless game where you can just wait for the nuts (aces) without risking anything. In this case, only sit at a table or register for a tournament with huge maniacs.
Note.
I mentioned that one possible explanation for ICM having an effect as early as hand 1, is that an early double up could affect the possibility of being overstacked in the bubble.
Another possibility is precisely the opposite, that given enough playing time (slower structure) as we approach the limits of an infinitely slow structure, an early double up has no effect in late stack size. The explanation would be that optimal play doesn't use this stack excess to maintain it or to increase the chances of reaching the final table or winning the tournament (especially in flat structures like satellites), but rather to survive. And in that scenario, if the second stack earned is used to fold and advance in the tournament while other players eliminate each other, then obviously it doesn't convert to $EV corresponding to the first prize, so it must be worth less.
Of course the second stack is going to be worth much less than the first one. But it isn't immediately obvious why, since neither stack is going to reach the final table (remember we are at the limits of an infinitely slow structure). It's rather that cEV and $EV are closer to each other when stacks are smaller, and the difference is the greatest when stacks are higher. As stacks become higher we reach tightness levels where our seat value is so high that we might fold kings against a similarly stacked opponent, and this effect exherts a pressure even on lower stacks, why would we want to double up if we are going to fold kings with that stack? It must not be a valuable stack.
In effect, having a small stack allows our stack distribution to shove without risking being overstacked and losing on a lot of dEV (delta EV, the difference between cEV and $EV). Under this analysis the value in the new chips gained can be useful again not in terms of cEV in order to increase our chances of being first, but just in terms of seat EV to allow us to survive longer.
Newer variables are needed to perform an analysis, not currently present in solver theory. The blind structure is a relevant parameter for decisions, as is the average stack (relevant for asymmetric stack size spots), variance in stacks, and 1st prize % ( for cEV value calculations), Bubble prize and %(as a proxy for payout steepness).
Blind structure MIGHT be simplified to the sum of blinds expected to be paid until ITM. E.g: on tournament A we have 100BB and 2000BB to pay until ITM, on tournament B we have 100BB and 200BB to pay until ITM. Ceteri paribus, regardless of how many players left till ITM, they would play very differently.
There is also the possibility that the gross amount of blinds paid is not as important as the amount of rounds left. In this scenario, our Expected stack increases when the blinds increase. Big stacks subsidize the smaller stacks by overfolding. And stack differences between small stacks like 5BB vs 10BB will not equate to a 2x chance of survival. In this sense the seat value usually associated with payouts also has a cEV value, which might explain why tighter ICM models are GTO even way before the Bubble. In a sense if we reach a new blind, we are reaching a bubble and experiencing a discrete jump in ($EV) payout. That is if we maintain a stack big enough for fold equity.
On fold equity I would distinguish between two types, one where we force the opponent to fold based on pot odds, that is, if we have 2BB, there's few scenarios where opponent folds to our shove. But a distinct fold equity would be by threat of elimination, one key feature of these different types of fold equity is that the first type is dependent on effective stack sizes as defined by modern solver theory as a function of stack size, big blinds and the smallest of the involved stacks. But the second depends on the well studied stack asymmetry, whereas the fold equity can be explained by merely replacing the effective stack by the two stacks in terms of big blind to stack ratio. (Of course a complete solution would involve payout structures, but we simplify assuming a constant ICM pressure).
While this first type of Fold Equity is what keeps stack sizes to the familiar 5-10BB range we usually see in tournaments, the second will depend on the stage of the tournament. The second is dependent on average stack sizes, and might or might not be worth pursuing.
There's probably a multimodal strategy distribution for stack sizes, if the average stack size is 30BB, and we have 15BB, we will probably not be in the 15BB range for long, we will probably converge into the 5-10 range or find stability in the 30BB range where we can exhert knockout pressure (reminder we are not considering knockout bounties).
And to propose a third mode, while we currently account for big stacks as a stack size that tends to reduce in size, the existence of a smallstack and an average stack implies the statistical existence of a big stack. Which is a good segway to recognize the existence of bullying and risk premiums.
The question then becomes, with the existence of several small stacks, mid stacks, and let's assume one big stack. Does the median stack size tend to decrease so that the mid stacks merge with the small stacks? Or does the median stack increase, such that the big stack overfolds for free survival, while the shortstacks enjoy a reduced risk of busting and the midstacks increase their mode.
One would be tempted to argue that the optimal strategy would be for the big stack to bully, but I first will say that this depends on the variable mentioned earlier, the first prize as a ratio to total prizes. The more top heavy of course, the more the big stack can bully. The flatter, the more the big stack is only useful in terms of increased survival. And on a related note, for those that might still argue that the big stack should still bully in a flat prize structure, in order to make effective their lead, be warned that in these free for all multiplayer scenarios, the loss of one player does not necessarily imply the win of another, bullying might benefit other players to a higher degree than it benefits the bully, so it's not sufficient to find that bullying is beneficial, the magnitude of this effect needs to be calculated.
The complexities in this line of thought are obvious, which is why my simplification of 1st % is so strong, if <50%, we assume overfolding is stronger than bullying, and thus that median stack sizes in general decrease, and thus the big stack decreases. Which would leave us with a bimodal distribution of stacks, which might find equilibrium until one player is eliminated and a new equilibrium needs to be found.
Some practical applications of this finds might result in plays that are widely different from predicted solver plays. For example, since solvers have a fixed and oversimplified parameter model, they vary their frequencies based on their cards, for this reason, they fold 23o very often, as they only shove that in 100% ATC ranges. However with a model that considers the variables mentioned in this post, we might find that the utility function of a 3BB stack is very low, and the utility function of a 8BB is more than double, so we shove ATC for 4BB. While to posit an extreme, if we have 10BB and are sitting at above average stack, we might fold 88 or AT from open raise from a shortstack UTG. Even if we are 5 levels away from the ITM. While we might shove that 88 if the average stack is 20BB, and even if our stack is 20BB and the average stack is 40BB.
As a final note, this style of play is grossly distinct from the recreational player's model which focuses on total prize pool and first prize, and might enjoy from (surprisingly) a lower variance.
BTW I lost the satellite. Jammed 5bb from SB with 23o and BB (40bb deep) called with 73s. 75th place.
We have several articles by Barry Carter exploring the ICM benefits of late registration:
However, this is for classic tournaments. As a general rule, you shouldn't late reg bounty tournaments because the
.
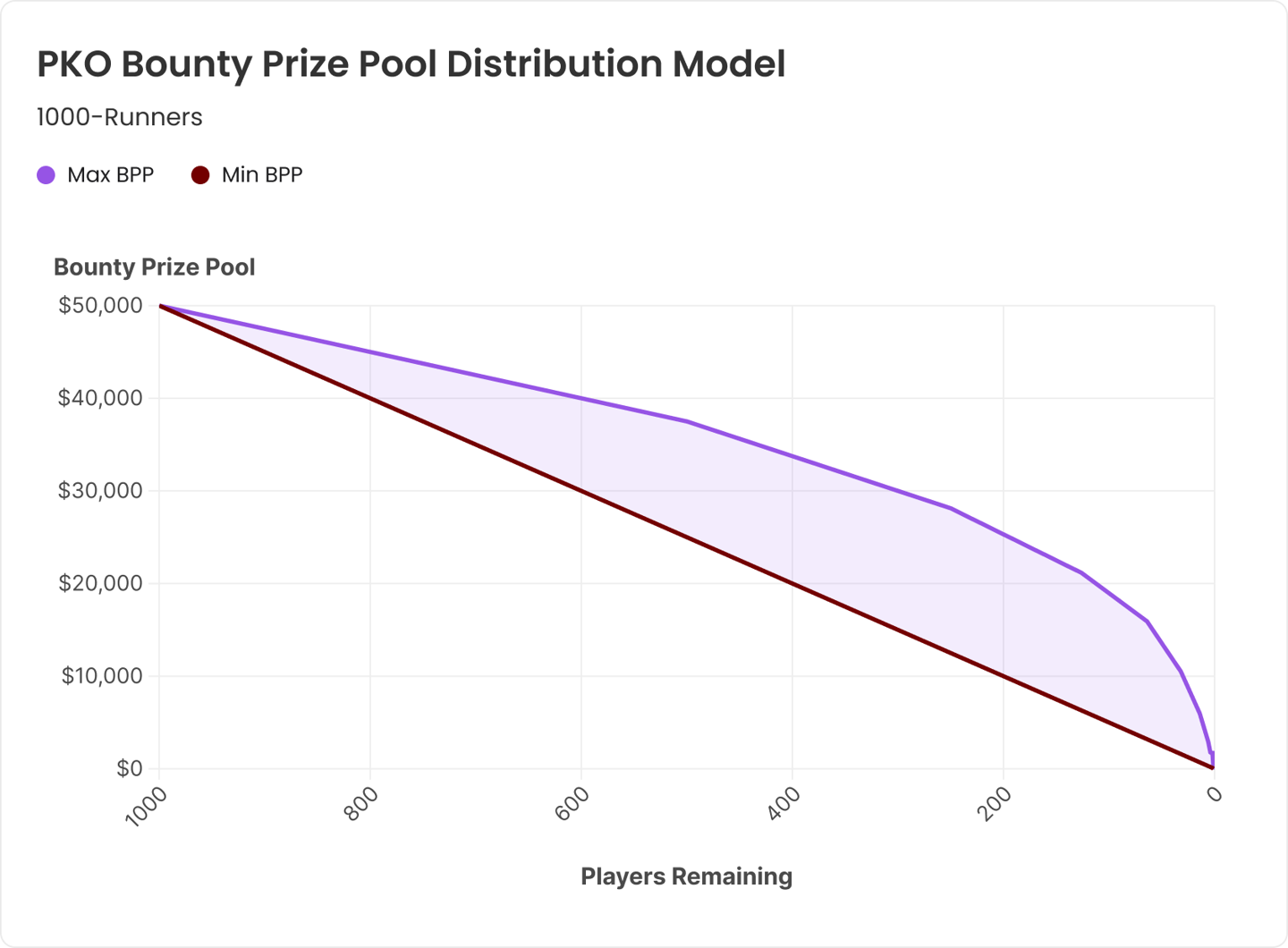
Not sure if this would be practically feasible. But what if the chips you get for buying in were correlated to the ICM value of the stack at the time of registration.
Ex. Instead of a $55 buyin getting you 10k chips at all times. What if the number of chips you received decreased as more people get knocked out, so basically, whenever you buyin, you get $55 worth of chips at the moment, based on ICM and % of the field eliminated.
You could also increase the buyin over time to get the same amount of chips, but I think having a constant buyin $ is more important than equal starting stacks.
Not sure if this would be practically feasible. But what if the chips you get for buying in were correlated to the ICM value of the stack at the time of registration.
Ex. Instead of a $55 buyin getting you 10k chips at all times. What if the number of chips you received decreased as more people get knocked out, so basically, whenever you buyin, you get $55 worth of chips at the moment, based on ICM and % of the field eliminated.
You could also increase the buyin over time to get the same am
The problem with this approach is that the average stack goes up with time, so you'd be starting shorter and shorter stacked. This already occurs but the effect would be amplified if you got less chips. It would massively disincentivise late regging and the casinos would never go for it as it would cut into the profits too much.
I personally don't see late registration as being that big of a problem, provided the late registration period doesn't go so incredibly late that people can still buy in when like 30% of the field is remaining. That's when it really gets to be ridiculous and the ICM effects become an unfair advantage. With a reasonable late reg period the ICM effects are pretty small. Like buying in late might be the equivalent of getting a rake reduction as far as the EV... nothing too major.
Personally though I think the unlimited rebuys are more of an issue when it comes to the integrity of the game. Again though the casinos just have no incentive to change the system and cut into their own profits.
As an aside, I used to play at a casino that had an "on time bonus" of 1000 extra chips on top of the 15,000 you normally started with. Basically they would just pass out an extra $1k chip to whomever was in their seat as the first hand was dealt. It wasn't a bad idea, although it could be a little frustrating if you got stuck in traffic or something. Other times they actually had a line and you could be there "on time" but not get your bonus because they were slow to get people seated. So no system is perfect.
Finally, an implication for Casinos and Tournament Organizers is that there needs to be some incentive for players to register early. Some casinos waive the rake, but I think this is not very clean accountability wise, the Casino still provides services to the player and should be paid for it. I think the best way to fix this would be to pay a bonus in chips to players that arrive on time.
It is even possible, especially as a stage 2 implementation, to change the bonus based on the level. So as t
I alluded to this in one of the rambles.
The idea is that you want to keep things simple. Even if the ideal is to have a perfectly continuous chipstack function, that would be confusing to players, it would invite distrust and unfairness.
Any casino or cartel of casinoes should start with a simple bonus for on time or even early registrations. Again this is not something unique, in many walks of life there is a natural incentive to be on time or to reserve with anticipation.
The second stage would be to reduce the bonus with each level. While technically feasible, varying stack sizes mid level would require more training for staff and more variables to account for, I don't think it's worth it. By reusing an already existing discrete time step in blind structures we make the whole thing much simpler, we don't need to introduce additional complexity here.
I'm not sure if table dealers or TOs should be awarding the bonus, can go either way.
Finally notice how I'm always wording this as bonus chips and not chip penalties. It's psychological and has no impact in theory, but I'm sure it will have much more acceptance if worder and structured this way. That is if the starting stack is 50K, you get 3.5K bonus, or a 3K bonus in the second level, and so on. The round number is for late reggies and the awkward number is for early reggers.
With regards to the ratio between bonus to stack, I think it should be very small around 5%. As even a very small amount is enough to make the optimal strategy being to play earlier.
The underlying problem is not so much that it affects players who sign up early, but ironically that it affects players that want to play optimal strategy, and are forced to not play the game. So even a 5% advantage or even lesser advantage, added perhaps with edge benefits and why not just having fun, will be enough to sway people in the direction of early reg. All the while giving very little reason for late reggers to complain.




