Should hero bet this flush-completing turn given the high hand bonus implications?

The EV of checking would not go up that full amount, because someone may call if you bet, and then you could still hit the bonus.

I believe that possibility (villain calling the bet) is included when calculating the EVs of betting/checking the turn.

Doesn't look like it to me.

I believe it has to be included because the EV of betting/checking the turn is calculated by working out the average expected return of the action given all possible continuations of the hand, which of course would include villain calling the bet a significant chunk of the time.

It's a nut changing card. Just bet small, like 40% pot. The high hand overlay is just bonus EV.

I would keep betting around half pot. If the pot was super small, say a 4 way limped pot I would start checking down flop to try to hit it.

Thanks guys yes for sure if there is no high hand bonus it's a very simple value bet, although I'd argue that in theory a larger size than 40-50% pot should be used, as hero is fully polarized.

What I'm trying to figure out is whether or not checking is higher EV than betting due to the extra $22 from the high hand bonus. I believe that to be the case (although I'm not sure) and if it is the case then I believe hero should check 100% of the time.

Another interesting question is how this would impact hero's turn strategy (although admittedly it's probably not by much) because it would mean that all straight flush draw combos would be checking, i.e. KT, KJ, JT, J8. This would very slightly reduces the semi-bluff portion of hero's turn betting range, making him fractionally more value-heavy if he changes nothing else, and I assume meaning that he has to bet a slightly tighter range (less value as well, in order to compensate). Also, it means that if hero does bet turn and gets called and the river completes a straight flush draw, then villain could in theory get ultra-aggressive because hero can never have a straight flush after he bets the turn. So I guess this would mean that hero would have to balance in some way and bet each combo a fraction of the time, in order to avoid this exploitative play from villain.

Don't know what you're talking about here. You told us how you calculated it.

"My odds of hitting it on the river are 45 to 1, which I assume increases the EV of checking by about 1000/45, or around $22.22."

I was talking about when the EV is calculated for betting/checking the turn, ignoring the high hand bonus.

When the EV of those decisions is calculated, it involves working out the average expected return for each decision, given all the possible ways in which the rest of the hand plays out. The line where villain calls the turn bet (which is what you mentioned) are included when the EV calculation is made for hero's options on the turn; check or bet. As I mentioned, usually the EV for these decisions is pretty close, and if checking was to have $22 added to it then I imagine it would become the clear better decision.

Here's an example of what I mean; I set the hand up for a solve in Piosolver:

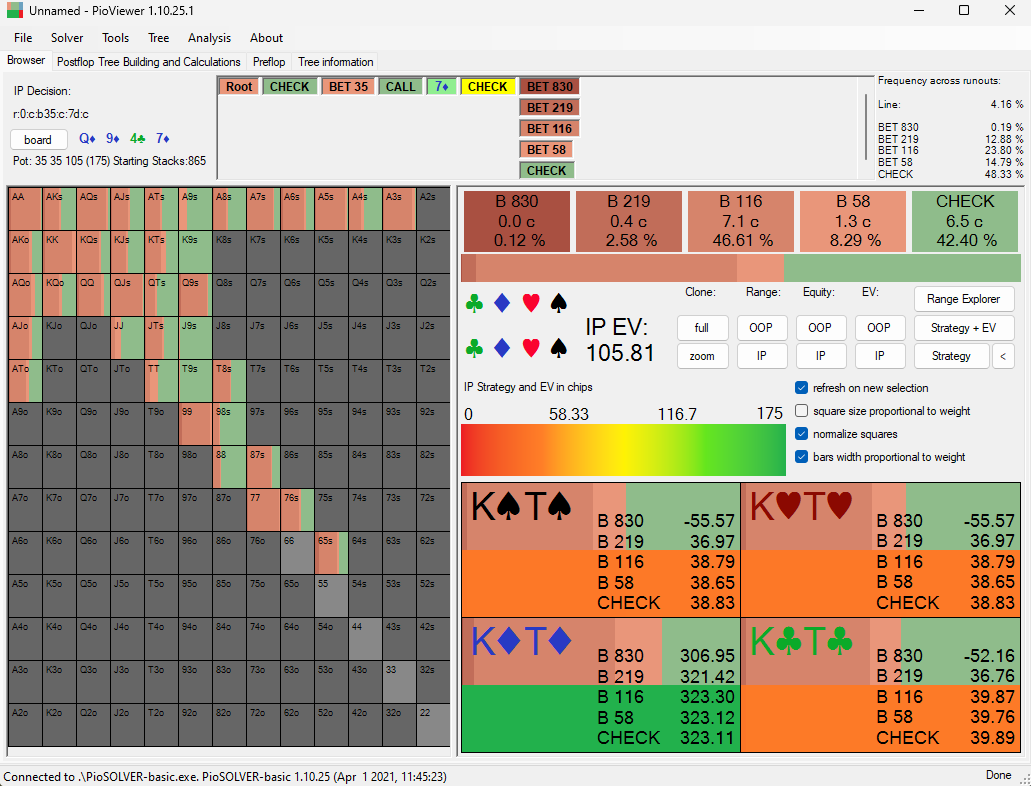
As you can see, the EV of hero betting the turn for various sizes is pretty similar (with the exception of jamming, which would obviously be an error with large EV loss):

Bet 830: EV 307
Bet 219: EV 321
Bet 116: EV 323
Bet 58: EV 323
Check: EV 323

(N.b I was way out with my estimation of what exact value the EV would be, my bad).

Now let's say we add $22 to the EV of checking, which I assume we can do given the possibility of hitting the high hand bonus. Then the options would look like this:

Bet 830: EV 307
Bet 219: EV 321
Bet 116: EV 323
Bet 58: EV 323
Check: EV 345

The EV of checking is clearly the best option, and by a large margin.

This effect is even moreso the case on the flop:

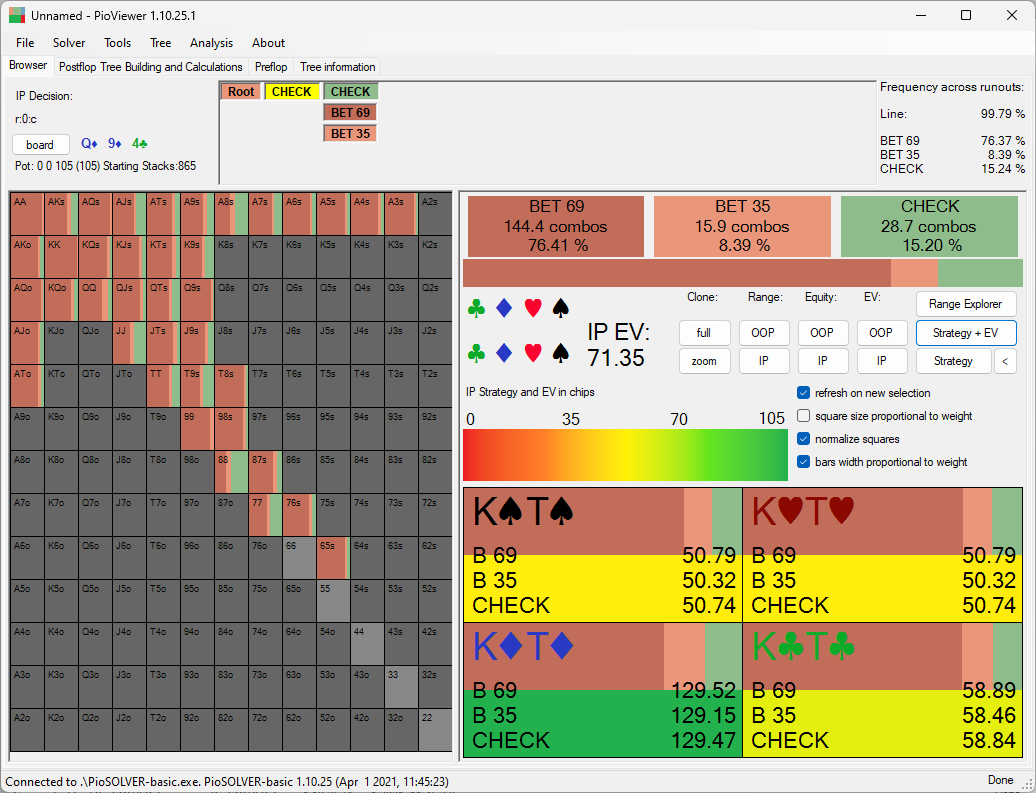
Bet 69: EV 129.52
Bet 35: EV 129.15
Check: EV 129.47

Adding the EV gained from checking brings the EV to 151.47; which again makes it clearly the best option.

The takeaway is pretty obvious: when you have even a one outer to hitting a 200bb high hand bonus, you should check rather than bet (unless the pot is gigantic, and with deep stacks behind - in which case there is a chance that the EV lost in checking would be greater than the EV gained in checking).

As played in the hand, I bet $100 and villain folded. I now believe that this was clearly a mistake, given the EV of the various options:

Bet 830: EV 307
Bet 219: EV 321
Bet 116: EV 323
Bet 58: EV 323
Check: EV 345

This may not look like much, but it's a pretty huge EV loss for a single hand.

i do think you're onto something here and tbh i thought it was wrong when i read the op. it should add some (lesser than 20 and probably unquantifiable) amount of ev to the turn bet node too

Nope, doesn't need to go to showdown, just needs to be tabled.

Ah, so you're saying the high hand bonus would also increase the EV of betting the turn? That definitely makes sense.

i mean it has to right? some amount of the time he calls down or whatever and you still get the bonus

i think the river sizing implications if you actually river a straight flush are really interesting too - its conceivable if he checks the river too (after turn goes x/x), even risking minbetting is a huge punt

nvm saw the tabling part and i get it

its not the greatest way to look at stuff but bear with me (the flop is multiway so hes supposed to be stronger ott but are people actually? idk man) but if the hand doesn't have to go to showdown the ev added should be your 22*w/e frequency he gets to the river? so it might influence your turn sizing options ie u want to choose a smaller size bc he "has" to peel wider if things are truly indifferent but its not going to be a 22$ difference between turn x and betting say 1/4 of pot or something

Certainly, that makes sense (although I am unsure how exactly solvers calculate these things, but what you said certainly sounds reasonable). This would mean that the EV gained in checking would be a little less than what I posted - but I imagine checking would still be the clear favored option in terms of EV and the dominant strategy.

I'd say some players (the decent ones) have stronger ranges multiway, but the majority are inelastic.

$22*w/e frequency he gets to the river makes sense. So for checking this would be the full $22, and it would decrease in an inversely proportional relationship with the betsize used. Certainly betting quarter pot would have an EV pretty close to $22 for the high hand bonus as well, because villain is going to call so wide. Given that the turn betsize EVs are so close:

Bet 830: EV 307
Bet 219: EV 321
Bet 116: EV 323
Bet 58: EV 323
Check: EV 345

This obviously warrants using a small size/checking as clearly the best options, because betting larger does not increase EV (the largest two options are lower EV than the smaller options), in addition to the fact that betting larger reduces the frequency with which villains calls, therefore also reducing the high hand bonus EV.

im not sure how to even try to calculate it. i guess the best way would just be add his turn call % * 22 to each of the betting options, but yeah equilibrium probably shifts towards check w this bonus size

suppose comedy option is conceivably very small sizes become the best option. run it from just the turn and give it like 10% as an option

I ran another solve and this time gave it four betsize options on the turn - 125%, 66%, 25% and 10%:

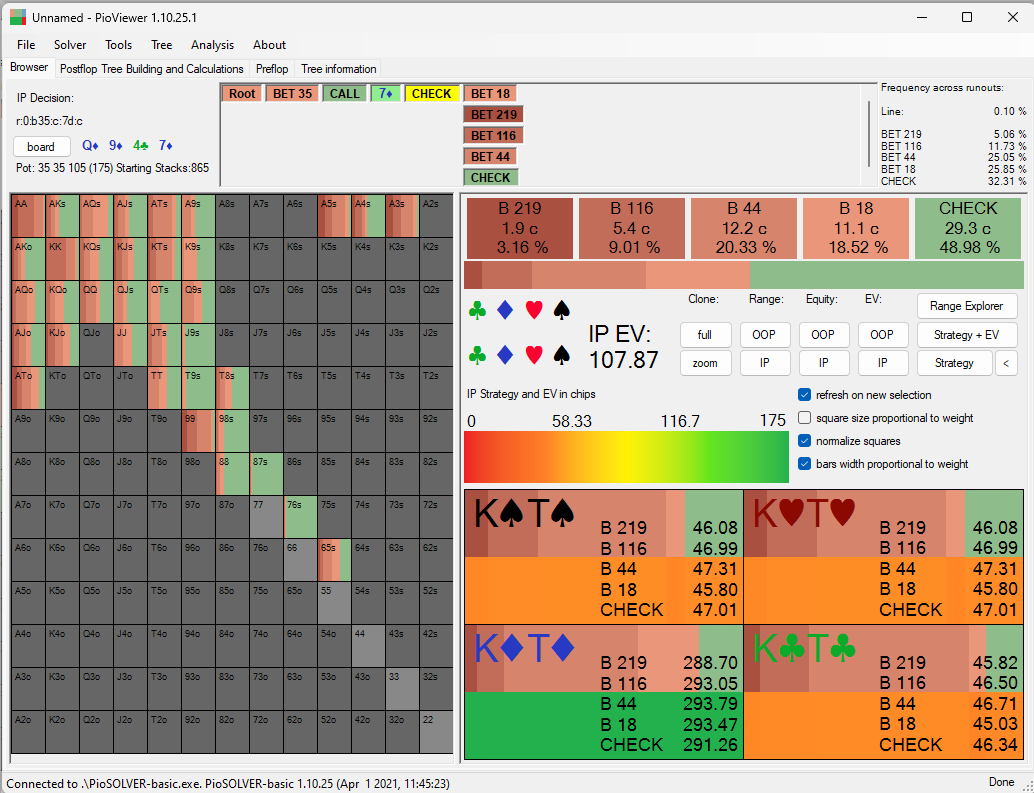
Something we didn't consider is that villain can also check-raise, and in that case the check-raising percentage can also be added to the call percentage in order to arrive at the percentage of the $22 high hand bonus that is added to hero's EV when betting the turn. This is how villain responded to the turn bet in the solve:

Vs bet 219 Villain calls 27.24% (and raises 7.82%)
Vs bet 116 Villain calls 43.06% (and raises 7.19%)
Vs bet 44 Villain calls 45.59% (and raises 21.21%)
Vs bet 18 Villain calls 51.39% (and raises 31.39%)

The EV of using different bet sizes for hero on the turn is as follows:

Bet 219: 288.70
Bet 116: 293.05
Bet 44: 293.79
Bet 18: 293.47
Check: 291.26

The possibility of hitting the high hand bonus adds some fraction of $22 to these EVs. However, if we bet, then that $22 is only realized when villain calls/raises. This means that we can add the EV of the high hand bonus as a proportion of how often villain calls/raises (assuming we never 3bet). This gives the following:

Bet 219: 288.70 + 35.06% of $22 = 296.41
Bet 116: 293.05 + 50.25% of $22 = 304.105
Bet 44: 293.79 + 66.8% of $22 = 308.47
Bet 18: 293.47 + 82.78% of $22 = 311.68
Check: 291.26 + 100% of $22 = 313.26

So the decision is closer when we include the high hand EV in the EV of hero betting the turn, but checking is still clearly the best option.

Note that betting smaller has the additional advantage that villain raises more often, which increases the percentage of the high hand bonus that is added to hero's EV when he bets the turn.

This is what I meant when I was telling you that checking would be worth less than $22.

The EV gained in checking is $22. The EV gained in betting is less than $22, and depends on the betsize. The bigger the betsize then the smaller gained in high hand bonus EV (because villain is more likely to fold).

looks like good work

Obviously I meant when compared with the EV of betting.

This is how I believe the high hand bonus increases the EV for hero's various options on the turn:

Bet 219: 288.70 + 35.06% of $22 = 296.41
Bet 116: 293.05 + 50.25% of $22 = 304.105
Bet 44: 293.79 + 66.8% of $22 = 308.47
Bet 18: 293.47 + 82.78% of $22 = 311.68
Check: 291.26 + 100% of $22 = 313.26

Checking realizes 100% of the $22 high hand bonus EV. Betting realizes a smaller percentage of the bonus, because villain folds x amount of the time, which means hero does not gain that extra EV. As can be seen in the EV of the different options listed above, this means that checking is clearly the highest EV option.

I don't even know what you mean by "hero is fully polarized" here. Like, as in, you have the nuts or nothing? What would your "nothing" be? Are you NEVER barreling with worse than a flush here? Like, NEVER? Not with QQ, or 99, or Q9, or AK with 1 diamond, or AdQx?

You have the 2nd nuts, you're the PFR, the FDFD came in on the turn, and 3 of the top 5 diamonds are accounted for. What the hell can an opponent have that will call a big bet here, when all your opponents limped in pre? You're basically hoping to get called by J8dd.

It's a nut-changing turn. In theory, V could have a lot of flushes in his range here. We know he can't, because we have KTdd, but *HE* doesn't know that. We *WANT* to give him a chance to raise off with his worse flushes, and any bluffs he might want to attempt. We also want him to call with all his OESD's with one diamond, and any 2P / sets he may have.

You should bet small, not big.

As for the additional EV from the high hand promotion - you shouldn't alter your play very much because of these promotions. The good news here is that if you bet small, V is going to fold less, and you STILL have the opportunity to improve to that straight flush on the river.

Ranges in poker can be polarized, linear or capped. A hand's polarization can be determined by the action of previous streets, because in general hero should be betting a polarized range from the flop forwards. If he checks at any point, for example on the flop, or on the turn after betting the flop, in theory his range becomes capped. In this hand, hero has iso-raised preflop, then bet on the flop and the turn. This means that his range is as polarized as possible.

Polarized ranges contain hands of nutted strength (for example on the board in the hand above on the turn, all flushes and sets) and hands that currently have zero showdown value; some of which can improve, and some that can't - i.e., total airballs. I am betting all of these hands on the turn as part of the standard polarized range that any decent winning player will be barreling across three streets.

My actual hand doesn't matter, it's the range that's important. This means that I bet large even when I am blocking some of the hands with which my opponent can call. If the turn in this hand had been a blank, then I would have used an even larger size (likely an overbet) as my opponent would have been capped from the flop. He's not capped on this turn, and therefore overbets are not the best option, but a larger size is still considered optimal in game theory because that's how polarized ranges operate. There are numerous game theory toy games that prove this to be the case, such as the clairvoyance toy game.

As you can see in the solver output I have detailed above, there is actually not that much EV difference when checking or using the smaller bet sizes (66% or 33%) on the turn:

Potsize is 175

Bet 830: EV 307
Bet 219: EV 321
Bet 116: EV 323
Bet 58: EV 323
Check: EV 323

(Note that these EVs do not include the EV gained for the high hand bonus).

The only way hero can really go wrong is to either use the overbet size (which he shouldn't use on the turn because villain's range is not capped) or to go all-in, which is an obvious mistake and incurs the most EV loss. That's from a solver's point of view. From a human point of view, most players are inelastic and are going to call large bets a lot wider than they should on this turn.

There are plenty of worse hands with which villain can call a large bet on the Q♦9♦4♣7♦ turn. You have to remember that this is live low stakes poker - people don't like to fold, and their limping can get wacky. For example, he can have Qx, 9x, JT, JJ, TT, flushes, Adx, a small amount of AA and KK, etc.

Villain is likely to raise his flushes in any case, and also likely to call with OESDs and two pair hands etc, given the size that I used. Betting smaller does not gain any additional EV.

As has been very clearly demonstrated above, hero absolutely should alter their play given the high hand bonus, as it significantly increases the EV of checking, to the point that it is clearly the dominant strategy and highest EV option. Doing anything other than checking is quite simply just losing EV.