TT vs likely NIT
The limp re-raise may have thrown me off. I highly debated about shoving turn, but pre-flop threw me, and then by the ri
Let's take a player with a 30% PFR over 5 hands and compare that with a player with a 0% PFR over 5 hands. The chances of being dealt a top 30% hand five consecutive times is 0.002%, while the chances of being dealt a bottom 70% hand 5 consecutive times is 17%.
To have a PFR of 30% over a certain sample doesn't mean that you have been dealt top 30% hands for every hand of that sample, that would give you a PFR of 100% for those hands (since you play all the top 30% hands, we'll ignore position for now). I'll change your example to 33% out of six hands in a row since it's impossible to play 30% out of five hands. To PFR 33% out of six hands you only need to get two top 33% hands out of the six hands, and the likelihood of getting that is way larger than 0.002%.
To have a PFR of 30% over a certain sample doesn't mean that you have been dealt top 30% hands for every hand of that sample, that would give you a PFR of 100% for those hands (since you play all the top 30% hands, we'll ignore position for now). I'll change your example to 33% out of six hands in a row since it's impossible to play 30% out of five hands. To PFR 33% out of six hands you only need to get two top 33% hands out of the six hands, and the likelihood of getting that is way larger than
You are absolutely right, but I don't believe that changes the relative likelihood of being dealt a playable vs non-playable hand.
Sent from my SM-A146U using Tapatalk
Alright, sorry, super busy so I'll keep this brief.
Opponent had - AdQd
The reason I said, likely NIT is because of the probability that Tombos and some others have mentioned. To the degree your opponent is on the outlier stats, you should be considering VPIP/PFR gap. When none exist like in this hand, I give higher probability that player is a "regular". I'm also looking at total hands and how much of an outlier are they from ideal stat ranges. 11/11 w/ ~35 hands means they are likely a reg that plays tighter. Probably on a slightly bad run of cards, but they have discipline. I don't and can't really deduce if they are a fish from that.
I'm also thinking that their limp re-raise range is probably extremely strong, and not just because fish will limp re-raise AA/KK, etc... but mainly because (assuming they are not a bot), have to be somewhat aware that they've been quiet at the table, and other regs have at the very least noticed this, even if they don't have tracking.
My main decision was on the turn. The river gets much easier because I'm just asking myself if this person, who is likely playing a very strong range, is bluffing more than ~30% of the time for their whole stack. Probably not, or they would be much more involved in the table earlier, and not just sitting back and waiting.
I was expecting AA/KK a lot, and AQ is probably at the bottom of their range here.
Alright, sorry, super busy so I'll keep this brief.
Opponent had - AdQd
The reason I said, likely NIT is because of the probability that Tombos and some others have mentioned. To the degree your opponent is on the outlier stats, you should be considering VPIP/PFR gap. When none exist like in this hand, I give higher probability that player is a "regular". I'm also looking at total hands and how much of an outlier are they from ideal stat ranges. 11/11 w/ ~35 hands means they are likely a reg that
Interesting result, thanks for that.
I think this is very likely a bot given the lack of VPIP/PFR gap and the fact that regs don't do much limp-RRing preflop. It's good to have some bot data for this line.
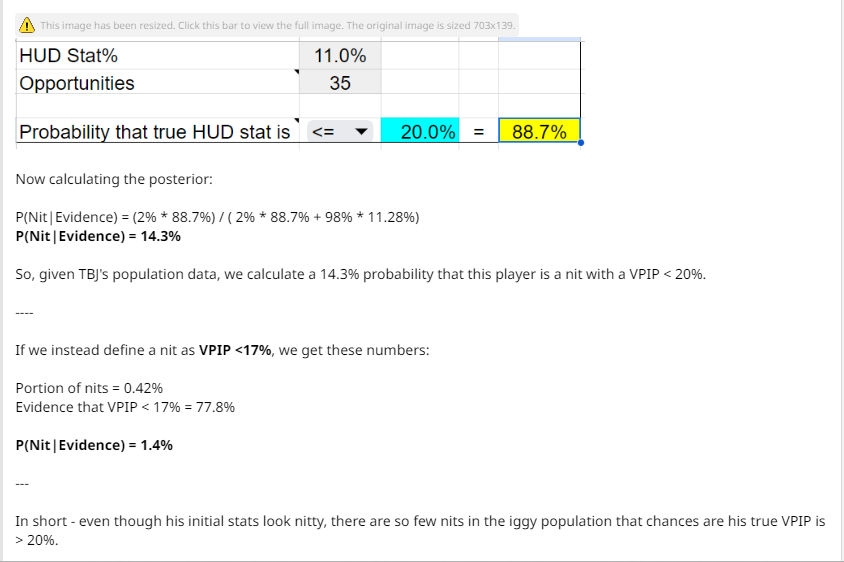
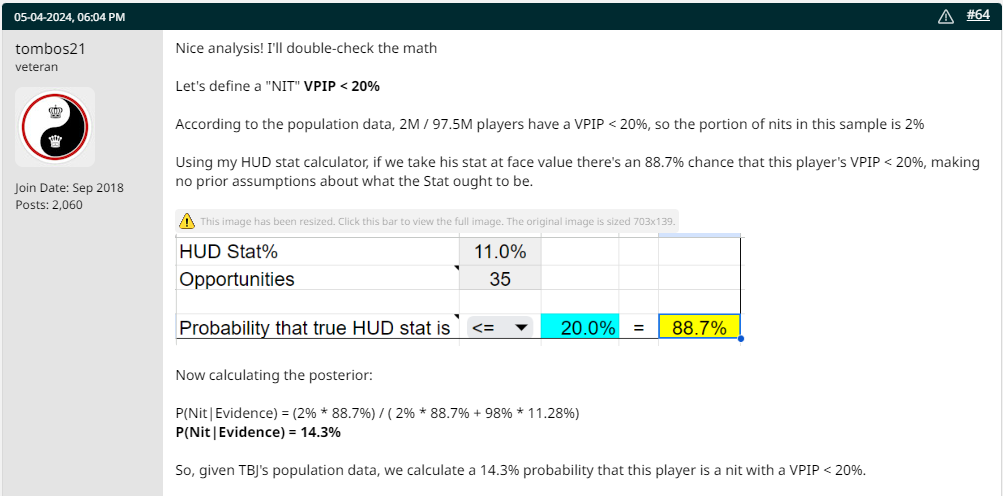
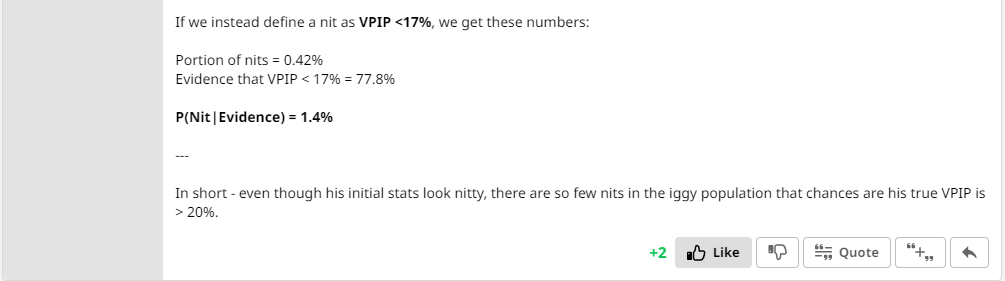
wrt to calling him a likely nit. Tombos concluded that it is actually very likely he is NOT a nit (if we define nit as <20VPIP).
Interesting result, thanks for that.
I think this is very likely a bot given the lack of VPIP/PFR gap and the fact that regs don't do much limp-RRing preflop. It's good to have some bot data for this line.
wrt to calling him a likely nit. Tombos concluded that it is actually very likely he is NOT a nit (if we define nit as <20VPIP).
Not sure where you're getting your reference, but from his post, it's about the same kind of Bayesian mean that I'd assume from just looking at VPIP/PFR and sample size. He said-
VPIP 17.3% ± 5.3%
PFR - 16.9% ± 3.7%
Which sounds about correct. I wouldn't personally remove only winning player data, because we have no idea about this player.
Not sure where you're getting your reference, but from his post, it's about the same kind of Bayesian mean that I'd assume from just looking at VPIP/PFR and sample size. He said-
VPIP 17.3% ± 5.3%
PFR - 16.9% ± 3.7%
Which sounds about correct. I wouldn't personally remove only winning player data, because we have no idea about this player.
Yes that was his calculation before he used Bayes Theorem based on TBJ's data. The first conclusion of Villain being a likely nit is based on selection bias.
This is why this thread is super important because we come to the counter intuitive conclusion of what you would normally think.
Here is his more in depth calculation in my PGC:
Discussion can be found here.
https://forumserver.twoplustwo.com/174/p...
*Final Conclusion: 14.3% chance of him being a nit
85.7% chance of him NOT being a nit
*If we define NIT as <20 VPIP
Limp/3b is so uncommon by a reg that I think it's safe to assume the nittiest possible range. Whether or not the guy is actually a nit preflop is kind of irrelevant.
Limp/3b is so uncommon by a reg that I think it's safe to assume the nittiest possible range. Whether or not the guy is actually a nit preflop is kind of irrelevant.
It's very unlikely it's a reg.
It's either a fish or a bot.
Since this player has no VPIP/PFR gap over 35 hands it is much more likely it's a bot. Which is why the actual results matter so much.
The nit/non nit preflop is an over arching statistical concept that goes way beyond this hand and show's how people can misinterpret seemingly straight forward data.
It's very unlikely it's a reg.
It's either a fish or a bot.
Since this player has no VPIP/PFR gap over 35 hands it is much more likely it's a bot. Which is why the actual results matter so much.
The nit/non nit preflop is an over arching statistical concept that goes way beyond this hand and show's how people can misinterpret seemingly straight forward data.
So you think bots do this with a super wide range? It's 11/11 so far so i think it's more reasonable to assume that the range is super tight and not random.
So you think bots do this with a super wide range? It's 11/11 so far so i think it's more reasonable to assume that the range is super tight and not random.
I was going over some bot hands with TBJ (he had 50nl-200nl data so maybe it's different at 1knl) and they seem to prefer trapping with strong hands and being more aggro with air.
Yeah the data is in this thread. The bot limp-RR range is wider than just top 2%-3% of hands.
Yes that was his calculation before he used Bayes Theorem based on TBJ's data. The first conclusion of Villain being a likely nit is based on selection bias.
This is why this thread is super important because we come to the counter intuitive conclusion of what you would normally think.
Here is his more in depth calculation in my PGC:
Discussion can be found here.
Ya... I appreciate the attempts there, and it's an interesting idea to add posterior population calcs, but I wouldn't rely on that data unless it was specifically for high stakes populations. You'll find a huge portion of people playing 70% VPIP + at micro stakes, and almost none at 1k+. I'm sure w/ accurate data at the higher stakes, it might make sense to apply (I'd have to give it some more thought honestly), but it's going to follow closer to Bayesian deviation rates on the whole. I think it makes more sense to not pollute the data, and instead assume that X player is going to play Y mean range, and based on sample size, they will normalize to Z% with expected hand distribution. It's a game of likelihood and in my mind in real time, I'm absolutely already considering the high end of their VPIP could be in the 22 range. But that's still going to make them tight, and unlikely they are playing 30%+ like I do.
Regardless, I think it's an important point to make in terms of small sample if you're playing in a pool w/ higher VPIP players and very small amounts of nits. It's more important to look at VPIP/PFR gap than it is to put high stock in the actual numbers. You should be trying to deduce whether they are more of a reg or a fish, and less so what their likely mean is for some of those stats in larger samples.
Ya... I appreciate the attempts there, and it's an interesting idea to add posterior population calcs, but I wouldn't rely on that data unless it was specifically for high stakes populations. You'll find a huge portion of people playing 70% VPIP + at micro stakes, and almost none at 1k+. I'm sure w/ accurate data at the higher stakes, it might make sense to apply (I'd have to give it some more thought honestly), but it's going to follow closer to Bayesian deviation rates on the whole. I think it
The data is filtered for VPIP<30.
If we used high stakes population data instead of 50nl-200nl data it would make it more likely he is NOT a nit not less likely because on average there are less nits at higher stakes. You can apply low stakes/mid stakes data to 1knl you just need to adjust it a bit.
I think it would be a mistake to dismiss or not use the data even if it's at lower stakes, it's still very relevant.
Anyways, that's all I'll say about that. It was a very cool hand and thanks for posting it. And I highly suspect that this is bot play.
The data is filtered for VPIP<30.
If we used high stakes population data instead of 50nl-200nl data it would make it more likely he is NOT a nit not less likely because on average there are less nits at higher stakes. You can apply low stakes/mid stakes data to 1knl you just need to adjust it a bit.
I think it would be a mistake to dismiss or not use the data even if it's at lower stakes, it's still very relevant.
Anyways, that's all I'll say about that. It was a very cool hand and thanks for pos
Edit- nm, missed you said it was filtered for < 30% VPIP.
But regardless, where did you get this calc, because it's basically saying that using bayesian mean calcs for expected stats is useless unless you have pop data. Which is just kinda strange honestly. But again, I need to give it some more thought.
My initial thoughts are it's not helpful to layer this pop data, simply from a human psychological perspective. Even if we say there's only 1 NIT in a population of 1 mill players in your pool. It's very possible that other players outside of that overal NIT range are just playing super tight for today, or the next 1k hands.
That's not quite how your calculation works. It's proportional, so also having less maniacs and players playing high VPIP will increase the NIT%'s.
But regardless, where did you get this calc, because it's basically saying that using bayesian mean calcs for expected stats is useless unless you have pop data. Which is just kinda strange honestly. But again, I need to give it some more thought.
I'm not claiming to be an expert in statistics but you can't just look at the VPIP/PFR over a small sample size and say okay that guy is a nit.
You need to look at the population data and figure out how how many guys with a true VPIP/PFR <20 are there in the population? Okay 2.5 million/97.5 million = ~2.5%
So it's much more likely it's a regular running bad than a real nit player once you do all the calculations.
This happens all the time in MDA, you look at a fish who under XR flop so you think XR-B-B is underbluffed but it's overbluffed because they don't give up enough. Everything is conditional probability so you need to look at multiple data points to come to your conclusion.
Maybe Tombo's or TBJ can come back in this thread, they can explain it better than I can.
I'm not claiming to be an expert in statistics but you can't just look at the VPIP/PFR over a small sample size and say okay that guy is a nit.
You need to look at the population data and figure out how how many guys with a true VPIP/PFR <20 are there in the population? Okay 2.5 million/97.5 million = ~2.5%
So it's much more likely it's a regular running bad than a real nit player once you do all the calculations.
This happens all the time in MDA, you look at a fish who under XR flop so you think
But that's what the Bayesian theorem is doing. It's giving you a standard deviation based on the likelihood you've run cold or good. It's very straight forward. There's no ambiguity.
Layering this MDA data on top of that, just doesn't make sense to me. It's like taking hard data, and then bending it into a narrative based on anecdotal evidence. And whether there's 1 player with 60k hands playing like a nit, or 150 players w/ 100 hands each, all of that will matter if you're trying to create a secondary table that will skew the likely distribution based on ratios.
And yes, you should never say something with certainty in a game of incomplete information. It's just one more piece of likely information when you're trying to reach a sound conclusion.
But that's what the Bayesian theorem is doing. It's giving you a standard deviation based on the likelihood you've run cold or good. It's very straight forward. There's no ambiguity.
Layering this MDA data on top of that, just doesn't make sense to me. It's like taking hard data, and then bending it into a narrative based on anecdotal evidence. And whether there's 1 player with 60k hands playing like a nit, or 150 players w/ 100 hands each, all of that will matter if you're trying to create a sec
If you aren't looking at population data when thinking about labeling VPIP/PFR as nit/reg/fish then the analysis is incomplete. You are missing information because the pool isn't random but you are treating it like it is random.
Anecdotal evidence is low sample evidence by definition, population data is high sample evidence.
It's like looking at a cold call % and saying oh this guy is a fish because he cold called but you aren't taking into account that there are more regulars at a table on average than fish.
Population data always has to be factored into the equation.
If you aren't looking at population data when thinking about labeling VPIP/PFR as nit/reg/fish then the analysis is incomplete. You are missing information because the pool isn't random but you are treating it like it is random.
Anecdotal evidence is low sample evidence by definition, population data is high sample evidence.
It's like looking at a cold call % and saying oh this guy is a fish because he cold called but you aren't taking into account that there are more regulars at a table on aver
Respectfully, I don't think you're understanding what Tombo's calculation is.
Maybe he, or someone familiar w/ this data can speak to it better.
There could be very valid reasons to layer pop data on top of stat probabilities. I just can't think of any right now. I'm open to hearing some good arguments.
Respectfully, I don't think you're understanding what Tombo's calculation is.
Maybe he, or someone familiar w/ this data can speak to it better.
There could be very valid reasons to layer pop data on top of stat probabilities. I just can't think of any right now. I'm open to hearing some good arguments.
It's definitely possible I am misunderstanding something but I've looked over it a bunch of times.
Let's put it this way, why would you not use population data on top of your stat probabilities? It will only make the HUD stats more accurate.
I'll message Tombos and see if he can come into the thread again.
It's definitely possible I am misunderstanding something but I've looked over it a bunch of times.
Let's put it this way, why would you not use population data on top of your stat probabilities? It will only make the HUD stats more accurate.
I'll message Tombos and see if he can come into the thread again.
I tried to make an analogy in my previous message using the anecdotal evidence reference. I don't think you understood that, and it probably wasn't the best analogy.
I think you know I'm all for using MDA data... this is just a place that it doesn't make any sense to do so, and actually makes the result less reliable.
I'll have to return to this tmw.
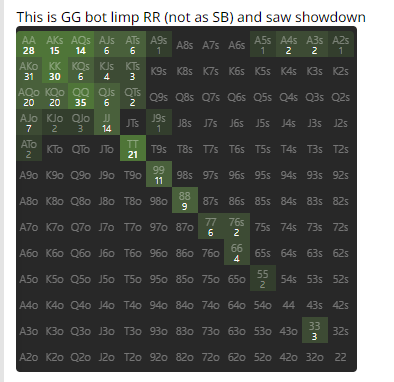
regs open limp 0.1% and re-raise 16.9%
fish are 17.2% / 5.2%
GG bot profile is 1.7% / 77.5%
so fish limp 172x more than regs, and the bot limp re-raises 80x more than regs
You will see some 18-20ish range VPIP tight players that try and feast on whales and gamblers at these stakes. They are mostly tight w/ their pre-flop range. Doesn't mean they won't bluff a lot post flop.
Couldn't those almost all be 22-26 VPIP regs running bad? You'd need both of you to stay at the same table for a loong time to be pretty confident in VPIP assuming this is based on Ignition
regs open limp 0.1% and re-raise 16.9%
fish are 17.2% / 5.2%
GG bot profile is 1.7% / 77.5%
so fish limp 172x more than regs, and the bot limp re-raises 80x more than regs
This limp RR data is crazy. So basically when someone limp RR's it is either a fish or a bot.
And if they have no VPIP/PFR gap it is a bot.
regs open limp 0.1% and re-raise 16.9%
fish are 17.2% / 5.2%
GG bot profile is 1.7% / 77.5%
so fish limp 172x more than regs, and the bot limp re-raises 80x more than regs
Couldn't those almost all be 22-26 VPIP regs running bad? You'd need both of you to stay at the same table for a loong time to be pretty confident in VPIP assuming this is based on Ignition
Correct... that's why I'd only say Nit/tight type player after a decent sample.
Here's a better explanation, and not sure why I couldn't explain this better earlier:
It's been a minute since I've taken a stats class in college, but you only want to apply Bayesian inference to Bayes theorem when the data model is not hard data. For example, when you're trying to derive the likelihood of someone getting a false cancer diagnosis based on mixed population data probabilities. When you have more finite data, you can essentially post adjust Bayes theorem to a more likely outcome.
But in this case, we have hard data, which is card distribution. What the population distribution is won't change the probability of card distribution to players.
It's like saying that if you flip a coin 1k times, it's 50% likely it will land on heads +/- 1%.
But if you have a guy in a hat w/ a sick hipster stache, and he flips it 1k times, it's 55% likely it will land on heads +/- 1%. Because of course, he has a sick stache.
Bayesian inference is only helpful when it adds more evidence that can assist in the conclusion. And maybe there's some post population adjustment that could be added (that's why I took pause at this to begin with), but it wouldn't radically alter the data, which is hard data in the form of card distribution.
Isn’t limp reraise UTG much more viable (as in, good) as rake decreases? I'm sure I've seen that discussed somewhere
And doesn't MDA drop off a cliff at higher stakes anyway? As the environment tightens to approximate GTO, and 5/6 players are decent regs potentially mining esoteric lines for adv, what's the use in applying lower stake exploit metrics?
Isn’t limp reraise UTG much more viable (as in, good) as rake decreases? I'm sure I've seen that discussed somewhere
And doesn't MDA drop off a cliff at higher stakes anyway? As the environment tightens to approximate GTO, and 5/6 players are decent regs potentially mining esoteric lines for adv, what's the use in applying lower stake exploit metrics?
I don't think any HS regs limp, but maybe there's guys in anonymous games who will do it with just AA/KK
It's a limp spot so not at all GTO, but also https://saulocosta.poker/7-are-nosebleed...
Isn’t limp reraise UTG much more viable (as in, good) as rake decreases? I'm sure I've seen that discussed somewhere
And doesn't MDA drop off a cliff at higher stakes anyway? As the environment tightens to approximate GTO, and 5/6 players are decent regs potentially mining esoteric lines for adv, what's the use in applying lower stake exploit metrics?
Open limp almost never happens, that's why I posted the hand and was a little thrown off when I was playing it. And yes as more of the pool understands GTO play, MDA goes down, but never away. 😀