Is Poker Zero-Sum or Non-Zero-Sum?
Dear Gents,
Let's do a little bit of math and philosophy...
The Case of the Tournament with Prizes Distributed Among the Top 3 Players
In a poker tournament where the top three players receive a portion of the prize pool, the dynamics change compared to classic zero-sum games. The main characteristic of a zero-sum game is that the sum of all players' winnings and losses must equal zero. However, in this type of tournament:
- The total prize pool is distributed among multiple players (not just one winner).
- Although losing players leave the tournament without a prize, the remaining players are not necessarily taking away an equivalent amount directly from their opponents as in a classic zero-sum game.
Is It Zero-Sum or Non-Zero-Sum?
The answer depends on the perspective. Let's consider two different viewpoints:
1. From the perspective of the overall tournament: If we look at the total prize pool, the game can be seen as zero-sum. The money put up by the players (the buy-in) is a fixed amount and is distributed among the winners. No new money is created, and the total winnings of the winners exactly match the sum of the buy-ins paid by all participants. In this sense, the tournament as a whole is zero-sum.
2.From the perspective of the individual players in the final stages: In the final stages of the tournament, players may adopt cooperative or non-cooperative strategies that can influence the prize distribution. For example, a player might try to survive as long as possible rather than go all-out for the win, in order to secure at least a portion of the prize pool. In this sense, player behavior can have aspects resembling non-zero-sum games, because there may be situations where all remaining players can "win" a share of the prize pool without necessarily immediately penalizing others.
Conclusion
A poker tournament with prizes distributed among the top three players can be considered zero-sum overall because the prize pool is fixed and distributed without creating or losing value. However, in the intermediate stages of the tournament or when viewed from the perspective of strategic interactions between players (such as adopting strategies to secure third place rather than risking it all to win first place), the game can exhibit non-zero-sum characteristics.
Thus, depending on how we analyze the situation—whether from a global or individual standpoint—the game can display elements of both zero-sum and non-zero-sum dynamics.
Opinions? ideas? Comments? all are very welcome...
Bye
24 Replies
For games with more than 2 players it's a distinction without a difference i think. Multiplayer games can display forms of cooperation even if they are zero sum.
Zero sum games are only special in the two player case, where you get strong "guarantees" about the NE / minimax / maximin solutions. That's not the case in multiplayer games, whether zero sum or not. Actually any multiplayer non-zero sum game with n players can be represented as a zero sum game with n+1 players, it's just semantics.
It is zero sum by definition. I think what you are thinking of is that hands are a sub game of tournament, and the strategy to win a hand is different than a strategy to win the tournament.
It just describes the impact of ICM.
Certainly there can be situations in a tournament where two (or more) players might have optimal strategies that would be suboptimal in a cash game. A simple and obvious example would be on the actual bubble, a short stack player shoves with 2BB and is called by two other players with 3BB. The two 3BB players still have 1BB remaining with potential action still open, but it is very unlikely that either of them will bet their remaining 1BB unless they have the absolute nuts. They both benefit immensely from busting out the all-in player. The best either can do by betting is to end up with a 5BB stack — if they win. The worst case is that by betting they will themselves bust out without cashing. Maybe it wouldn’t have to be the absolute nuts, but their betting range would be VERY tight in this spot. Even if they both check it down and the all in player wins, they both have 1BB left, so they both have decent chances of cashing (if the other busts first).
This doesn’t mean it isn’t a zero sum game, though. It just means that the benefit they get from busting out a shorter stack is greater than the potential benefit they might get from making a more optimal play in terms of chip EV. The EV of the cash payout is what is important in tourneys, not the EV of the chips won. The difference between them is the basis of the ICM model.
It's zero sum on the start, but ofc when ppl get knocked out it is not.
How so?
Remaining players complete for more money total than they put in.
That's not what zero sum means.
Zero sum means that when you add payouts of all the players it's zero.
If you are looking at the tourney as a whole (once registrations are closed) then the total payout does not change. When a person gets knocked out, their theoretical share of the payout gets distributed to those still left in the tourney. Nothing added, nothing lost.
If you are looking at individual hands, someone's equity in the tourney increases or decreases based on the chips added or lost to players' stacks. Nothing added, nothing lost.
If you are looking at the tourney as a whole (once registrations are closed) then the total payout does not change. When a person gets knocked out, their theoretical share of the payout gets distributed to those still left in the tourney. Nothing added, nothing lost.
If you are looking at individual hands, someone's equity in the tourney increases or decreases based on the chips added or lost to players' stacks. Nothing added, nothing lost.
This is correct. In money terms tournaments are zero sum. Looked at in terms of chips, though, there are stages of a tournament where the chips are not zero sum. Chips added to an already large stack typically have less value than the chips lost from a short stack. If a player with a 100bb stack busts one with 10BB, it is a net loss for the two players involved, and therefore a net gain for the rest of the field. (This is most clear if it happens on the bubble or at a final table where the player busting causes a pay jump for everyone else).
Conversely if a 10BB stack doubles up against the 100bb stack, the chips won by the short stack are much more valuable than the chips lost by the big stack. Therefore this is a net loss for the rest of the field (especially noticeable if you are a 9bb stack hoping to see a bust out that will either put you in the money or increase your payout).
This is correct. In money terms tournaments are zero sum. Looked at in terms of chips, though, there are stages of a tournament where the chips are not zero sum. Chips added to an already large stack typically have less value than the chips lost from a short stack. If a player with a 100bb stack busts one with 10BB, it is a net loss for the two players involved, and therefore a net gain for the rest of the field. (This is most clear if it happens on the bubble or at a final table where the playe
Isn't the bold the definition of zero sum?
I agree that in a tournament chips gained/lost do not correlate 1 to 1 with prize pool equity.
If you are looking at the tourney as a whole (once registrations are closed) then the total payout does not change. When a person gets knocked out, their theoretical share of the payout gets distributed to those still left in the tourney. Nothing added, nothing lost.
If you are looking at individual hands, someone's equity in the tourney increases or decreases based on the chips added or lost to players' stacks. Nothing added, nothing lost.
Sum of payouts of players left is now bigger than zero, so that subgame is not zero sum.
Sum of payouts of players left is now bigger than zero, so that subgame is not zero sum.
That isnÂ’t what zero sun means. A zero sum game for two players is one where when one player gains value it must necessarily come from the other player losing value. Take a splash pot for example. Suppose the house adds $100. If itÂ’s a 10 player pot, then prior to the deal each player has an EV of $10. Once the cards are dealt this will change. If I get AA in this pot my EV climbs to something like $32. The EV of everyone still adds up to $100 - the size of the pot (this is prior to any betting obviously and ignores blinds for simplicity). Where did my extra $22 of WV come from? It came from all the other players having an EV lower than the $10 they started with. The sum of the CHANGES in EV is zero for a zero sum game. It is not necessarily true that the sum of all EVs is zero.
Contrast this with a non zero sum game. In a non zero sum game each players EV changes as a result of their actions, but the sum of these changes might be positive or negative. Economic trades are a good example of non zero sum interactions. I have extra card that I donÂ’t want. Someone else needs a car and has extra money they can use to buy a car. I gain by getting money I need for other things, the other person doesnÂ’t lose, though. They value having a car more than they do having that extra money - itÂ’s a win for both of us. Such spots are not possible in poker. My gain is your loss, even if we both have positive net EV.
I was just thinking about the zero-sum thing also, and I asked myself: "Literally, where is this overall zero ?" I think it might had been gone forever, the same day someone cheated at poker for the first time or the first online freeroll was run.
I was just thinking about the zero-sum thing also, and I asked myself: "Literally, where is this overall zero ?" I think it might had been gone forever, the same day someone cheated at poker for the first time or the first online freeroll was run.
See my post above. Zero sum does not mean that the sum of expected values for all players is zero. It means that the sum of CHANGES to EVs as a result of a given action is zero. Just as a simple example - splash pot, casino adds $100 as a promo, 10 handed. Before cards are dwalt, each player has an EV of $10. Player 1 gets dealt AA. As a result, his EV (prior to any PF action) is now about $35. His EV rose by $25. The EV of the other 9 players collectively dropped by the same amount. This is still a zero sum game.
A non zero sum game is one where an action can be collectively beneficial (or harmful) to all players. Economic transactions, for example usually are win-win. I have extra money I donÂ’t immediately need; you own a business and need money to expand it, making it more profitable. We both benefit if I loan you my extra money; I get repaid with interest, you get the money you need to expand and make more future profit. I am unaware of any situation in any form of poker in which case an action is mutually beneficial to all players. Even collusion situations are zero sum - they certainly benefit the colliders, but it is at the expense of the victim.
In a tourney situation, consider a toy example. Three players remaining. Third place gets $200, 2nd $600, and 1st $1000. In the toy example all three have equal stacks. Each playerÂ’s EV is just 1/3 of the total prize pool, or $600. Suppose all three go all in, player 1 with KK, players 2 and 3 with AA, and the AA hands hold. Player 1 now has an EV of $200 - he busted out in 3rd. Players 2 and 3 each have an EV of half the remaining money or $800. Players 2 and 3 had a collective gain in EV of $400 ($200 each). Player 1 lost exactly the same amount of EV - from $600 to $200, for a $400 loss. It is zero sum.
In real tourneys, obviously, the EVs wonÂ’t be so easy to calculate; I made up my toy example precisely to make the calculation easy. The same principle still applies, though. One playerÂ’s EV gain comes at the expense of one or more of the other playersÂ’ EV loss. It is zero sum.
Ok, I just took a quick look at this thread without deeper analysis. I visualized "zero sum" as the sum of all poker profits and all poker losses in the world.
Like: (+$860 424 936.14) + (-$860 424 936.14) = 0
Typically your opponent's loss is equal to your gain. But that's not how it works in MTTs.
In tournaments, a HU pot is not zero sum since the ICM values of all players in the field can change. You don't claim 100% of the $EV you take from your opponent.
Here's an example from a 40bb symmetrical bubble spot. As you take chips of your opponent, some of their $EV gets "leaked" to the field.
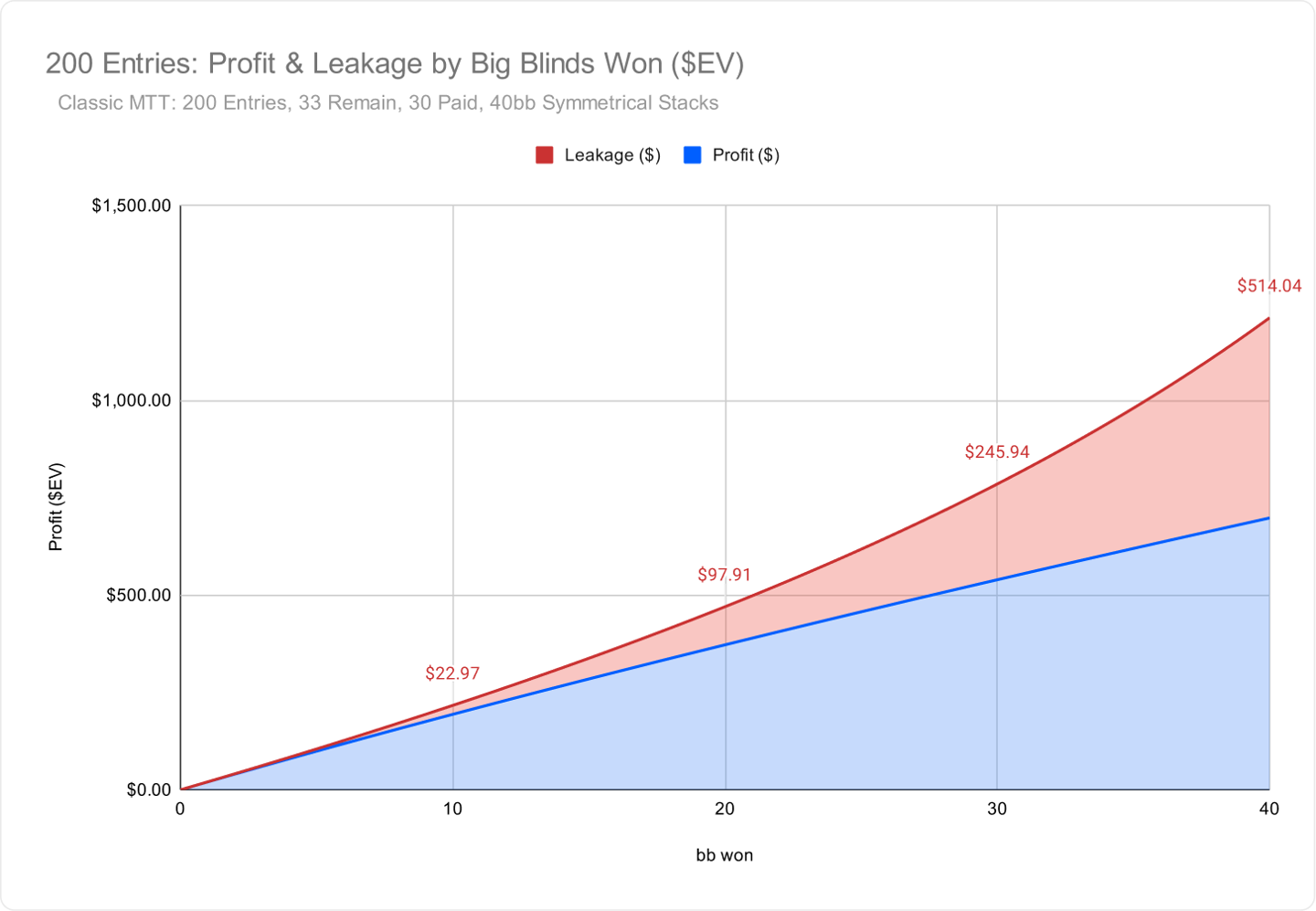
You can read more about it here:
Typically your opponent's loss is equal to your gain. But that's not how it works in MTTs.
In tournaments, a HU pot is not zero sum since the ICM values of all players in the field can change. You don't claim 100% of the $EV you take from your opponent.
Here's an example from a 40bb symmetrical bubble spot. As you take chips of your opponent, some of their $EV gets "leaked" to the field.
You can read more about it here:
True, but any EV gained by one player comes at the expense of the aggregate EV of all the other players in the tourney (and correspondingly any EV loss by one player causes an equal gain in the EV of all the other players in aggregate). When player A wins a pot from player B, AÂ’s EV increases and BÂ’s EV decreases. But depending on the stack sizes and the point in the tourney where it occurred, A might gain more than B loses or Vice-Versa. This does not mean it isnÂ’t zero sun, though. The EV of players C,D,E,F, etc. is also affected by the result of the hand. If A gains more EV than B loses, the rest of the field loses EV on aggregate. If A gains less than B loses the remaining field gains EV on aggregate. This is most clear at or near the bubble when player B has busted out. B loses all the EV he had before the hand, but it isnÂ’t all gained by A. The rest of the field gains EV, and most obviously so when B busts out on the bubble. It is still zero sum - the EV lost by B is distributed among the field and the EV gained by the field in aggregate (including player A) is equal to the loss of EV by player B.
(Note: in the above I intend EV to mean $EV, not chip EV. Tourneys are obviously zero sum in terms of chips - you can only gain chips if someone else loses them).
True, but any EV gained by one player comes at the expense of the aggregate EV of all the other players in the tourney (and correspondingly any EV loss by one player causes an equal gain in the EV of all the other players in aggregate). When player A wins a pot from player B, AÂ’s EV increases and BÂ’s EV decreases. But depending on the stack sizes and the point in the tourney where it occurred, A might gain more than B loses or Vice-Versa. This does not mean it isnÂ’t zero sun, though. The EV o
Yes, the $EV for the entire field is zero-sum, but not for the two players in a HU pot. And that is a problem because it changes the optimal strategy for those two players in that HU pot. You lose a bunch of guarantees in Nash, and you get weird things like giving one player more actions can actually lower both player's EVs.
Yes, tournaments are different than cash.

